Посоветуйте алгоритм по нахождению многоугольника
Построить выпуклую оболочку
Слишком много вариантов решения.
Можно сделать во-первых выпуклый, который подходит. А если невыпуклый, то вообще можно сделать, чтобы все точки лежали на границе.
В первом случае гугли по «алгоритм построения выпуклой оболочки»
Второе — выбираешь нижнюю правую точку, остальные сортируешь по полярному углу (равным по углу — по возрастанию расстояния соединяешь в естественном порядке (на последней прямой порядок обратный).
Можно сделать во-первых выпуклый, который подходит. А если невыпуклый, то вообще можно сделать, чтобы все точки лежали на границе.
В первом случае гугли по «алгоритм построения выпуклой оболочки»
Второе — выбираешь нижнюю правую точку, остальные сортируешь по полярному углу (равным по углу — по возрастанию расстояния соединяешь в естественном порядке (на последней прямой порядок обратный).
Почему именно изображённое решение желаемое? По какому критерию отбираются вершины в границу? В данном случае это не максимизация и не минимизация числа вершин, а также, судя по всему, не минимизация длины границы. Тогда что?
Я правильно понял, что задача имеет множество желаемых решений? В частности, что вот такие два решения тоже подходят:
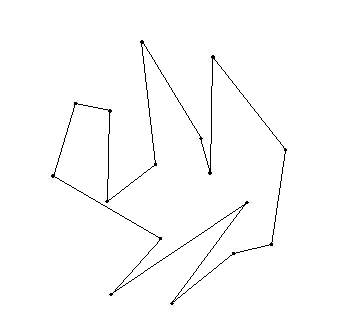
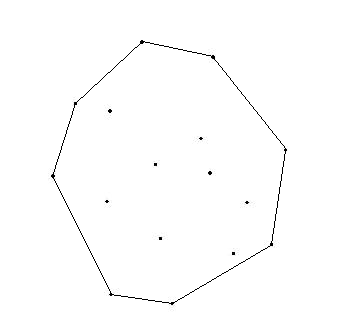


Во, а первое ты каким алгоритмом строил?
Извините, затупил. В такой постановке действительно много решений, и решение как на картинке тоже не единственное . Спасибо, мне подойдет выпуклая оболочка - она единственным образом определяется.
Во, а первое ты каким алгоритмом строил?Не знаю.
методом пристального взгляда (с) 

эх, Ионкин...
Хотя нет, вру, товарищи. Выпуклая оболочка не всегда подойдет. Цель этого всего действия - оценить площадь, занятую точками, в виде фигуры - многоугольника. Область предполагается односвязной. Хочется что-то такое:
Дано:

Решение:
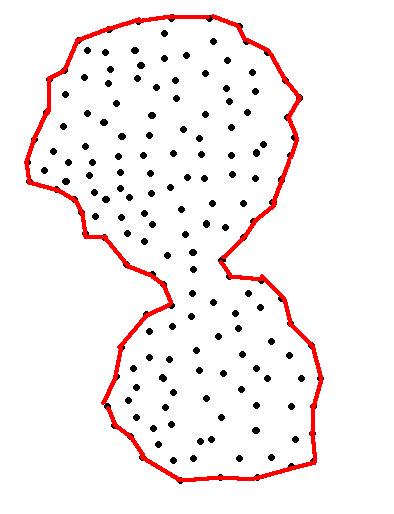
Видно, что выпуклая оболочка здесь не подойдет.
Как бы это сформулировать поточнее. Хочется найти такой многоугольник, который описывает односвзяную область, занятую точками (возможно, невыпуклую). Сходу критерий придумать не могу...
Дано:

Решение:

Видно, что выпуклая оболочка здесь не подойдет.
Как бы это сформулировать поточнее. Хочется найти такой многоугольник, который описывает односвзяную область, занятую точками (возможно, невыпуклую). Сходу критерий придумать не могу...
А обязательно многоугольником?
Просто корректной постановки пока ну вообще не видно.
Просто корректной постановки пока ну вообще не видно.
Да, постановка еще некорректная. Я и не знаю, как ее получше сформулировать. Описывать площадь желательно многоугольником, но не обязательно. Если многоугольником - может быть, придумать какой-то критерий, который к уже известному множеству граничных точек добавляет такую, что она не очень далека от уже имеющихся в множестве граничных, но и не слишком нарушает выпуклость. Крайние случаи - самая близкая или самая "выпуклая" - не подходят, т.к. в первом случае не пойми что получится, во втором - просто выпуклая оболочка. Вопрос в том, как правильно найти баланс между расстоянием и выпуклостью. Ну, может, это и не единственный вариант решения. Может, у кого-нибудь возникнут еще идеи.
PS. В тред призываются телепаты!
PS. В тред призываются телепаты!
получается надо искать баланс между двумя взаимоисключающими критериями: площадь - чем меньше, тем лучше и длина границы(выпуклость) - чем меньше, тем лучше.
Тогда мб что-то вроде S + l^2 -> min, с сохранением условия того, что остальные точки лежат внутри?
PS. Правда, хз, как решать такую задачу.
PS. Правда, хз, как решать такую задачу.
Просто если надо именно оценить площадь, то приходят в голову всякие методы типа превратить эти точки в окружности, посчитать суммарную площадь.
Тут встают вопросы: выбор радиуса, подсчет покрытой площади.
Тут встают вопросы: выбор радиуса, подсчет покрытой площади.
Нет, нужно оценить не только площадь, но и саму область (которая предполагается односвязной)
Если точек много, то можно чем-то вроде Монте-Карло подсчитать.
если точки лежат на сетке, можно шагающими квадратами их 

а как определять, что точка попала "внутрь"?
Тут встают вопросы: выбор радиуса, подсчет покрытой площади.
так это я не протвою методу спрашивал
Пока придумал построение многоугольника по методу Джарвиса , но сделать так, чтобы поиск следующей вершины был бы из множества тех точек, расстояние до которых от предыдущей не превышает чего-то.
как правильнее?
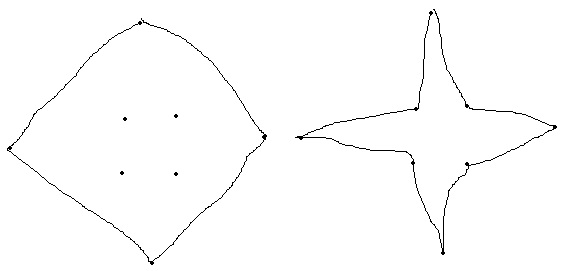

весовую функцию подправь.
пусть S - площать, l - периметр.
min(S + k*l*l k - параметризует весовую функцию.
пусть S - площать, l - периметр.
min(S + k*l*l k - параметризует весовую функцию.
Сейчас сложно сделать выбор, они почти одинаково приятны. Думаю, все-же второй вариант.
Но я думаю, что случаев с такими редкими точками не будет.
Но я думаю, что случаев с такими редкими точками не будет.
Если плотность точек высокая, то может действительно "наращивать" точки, пока не получим связную область, а потом из этого извлечь какую-нибудь информацию — площадь или "крайние" точки.
они почти одинаково приятныглазу?
Да, ведь я не придумал еще четкого критерия.
Проверкой соответствующих неравенств. (пространство бьется на квадратики, потом цикл по квадратикам)
Вообще, чего-то никаких характеристик множества точек не было приведено вроде б...
Вообще, чего-то никаких характеристик множества точек не было приведено вроде б...
Если плотность точек высокая, то может действительно "наращивать" точки, пока не получим связную область, а потом из этого извлечь какую-нибудь информацию — площадь или "крайние" точки.ага, в случае целочисленных координат - можно применить стандартный приём расширения с последующим сужением. Простенький фильтр, закрашивающий чёрным точку, если в r-радиусе её есть чёрная исходного изображения. А потом тоже самое для белых точек.
А если пиксельная обработка не годится - составить граф связности. Точки A и B связаны, если расстояние между ними не превосходит R. А дальше строить периметр с учётом того, что только связные точки могут лежать на одном ребре. Получится объединение выпуклых оболочек.
Вообще, чего-то никаких характеристик множества точек не было приведено вроде б...должно быть приятно глазу автора

Возможно оболочка с минимальной максимальной длиной ребра ему подойдёт. 

А чем не подойдет такой критерий выбора радиуса: минимальный радиус, при котором получается односвязная область?
Т.е. ты предполагаешь радиусы одинаковыми?
Да вообще не знаю, чем не подойдет любой метод вообще
Да вообще не знаю, чем не подойдет любой метод вообще

Мне очень нравится эта идея.
Она не будет работать для таких случаев:
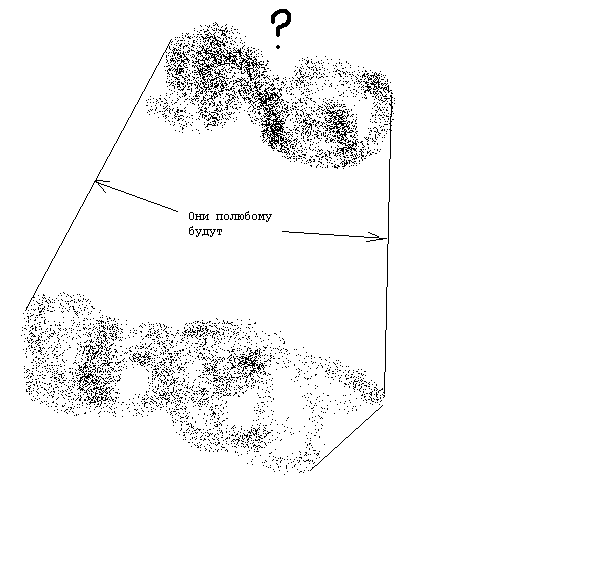
Она не будет работать для таких случаев:

Вообще, с радиусами этими плохой метод, наверное, потому что слишком большую прибавку по периметру будет давать.
Мне очень нравится эта идея.Так вроде автор хотел односвязную область. Если несколько областей есть, то их нужно отдельно выделять, конечно. А будет на самом деле как-нибудь так:
Она не будет работать для таких случаев:
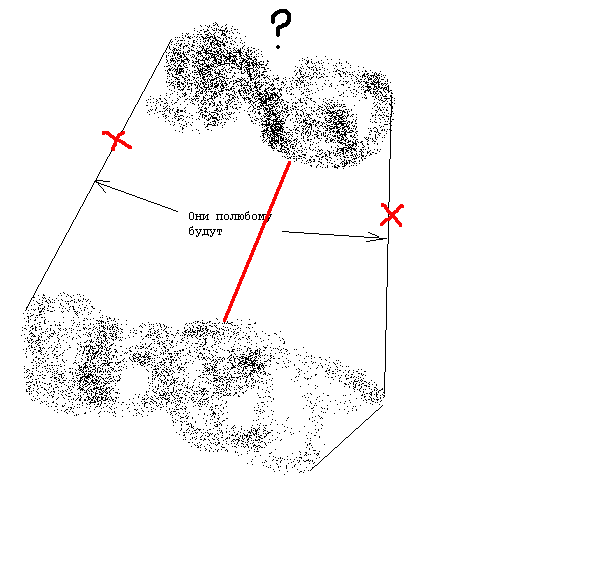
Эти две оторванные области — они у тебя в голове. Там-то дан набор точек.
Если несколько областей есть, то их нужно отдельно выделять, конечно.Односвязная область может быть несвязной.
Эти две оторванные области — они у тебя в голове. Там-то дан набор точек.Так я говорил про то, что автор вроде хочет одну область, а не про то, что ты 2 области нарисовал.
Односвязная область может быть несвязной.Ну я конечно неправильно написал. Вместо "одна связная" область написал "односвязная".

Но как односвязная область может быть несвязной не знаю.

Так я говорил про то, что автор вроде хочет одну область, а не про то, что ты 2 области нарисовал.Ну хотел одну — пусть одну и строит, тогда мой пример как раз против твоего алгоритма.
Ты хочешь сказать, что там точки довольно плотно расположены по всей области? Я же говорю, подход нравится мне твой, для довольно широкого класса точек будет работать на ура, вроде.
Но как односвязная область может быть несвязной не знаю.А это я тупанул, не может, конечно.
А это я тупанул, не может, конечноотличный способ привлечения внимания к треду!
я аж возмутиться про себя успел

тогда мой пример как раз против твоего алгоритмаТак мне интересно почему против. Если область одна нужна, то там такая фигура и будет как ты нарисовал.
А я предлагал не алгоритм, а формализацию цели.

Алгоритм вот с графом под такую цель хорошо подойдёт, наверное.
А я предлагал не алгоритм, а формализацию цели.Да это я все описываюсь. Понятно, ты предлагаешь постановку.
Так мне интересно почему против. Если область одна нужна, то там такая фигура и будет как ты нарисовал.Ну потому что эти длинные ребра уже и будут минимизировать максимум, как соединять остальные — эта постановка никакой информации не дает.
Ну потому что эти длинные ребра уже и будут минимизировать максимум, как соединять остальные — эта постановка никакой информации не дает.Ну там пофигу чем, главное, чтобы рёбра оболочки были не длиннее этих крайних. В таком случае да, детализация границы пропадёт, т.е. средние по размеру "впадины" "накроются" прямыми рёбрами.
В таком случае да, детализация границы пропадёт, т.е. средние по размеру "впадины" "накроются" прямыми рёбрами.Да нет, все еще хуже. Там вообще нет иформации. Т.е. любая оболочка, содержащая эти ребра (и да, более короткие) подойдет. Там чтобы просто накрыло впадины, надо еще критерии добавлять.
Там чтобы просто накрыло впадины, надо еще критерии добавлять.Согласен. Я же не всю задачу этим предлагал формализовать. Это только дополнительный критерий "красивости".
А в качестве оболочки вполне можно взять внешний контур графа.
внешний контур графа.какого?
Я же не всю задачу этим предлагал формализовать. Это только дополнительный критерий "красивости".Да оно хорошо должно работать для точек, которые нарисовал автор, например. Может ему и подойдет, только еще решить проблему надо

Берём полный граф, из него выкидываем все длинные рёбра.
Я вот только думаю — а не может ли там пересекающихся рёбер получиться.
Я вот только думаю — а не может ли там пересекающихся рёбер получиться.
Я вот только думаю — а не может ли там пересекающихся рёбер получиться.ну как минимум их можно даже честно обработать (теоретически т.е. объявить точку пересечения вершиной искомого многоугольника.
отличный способ привлечения внимания к треду!Я так делал на этом форуме уже раза три. И этому есть объяснение: у меня тупой глюк в мозгу, я помню, что односвязность — это про стягиваемость любого контура, а что связность уже нужна для понятия области — забываю.
я аж возмутиться про себя успел
ну как минимум их можно даже честно обработать (теоретически т.е. объявить точку пересечения вершиной искомого многоугольника.А вдруг низзя?

 заставил задуматься
заставил задуматься 
Ну да, там как минимум довольно сложно может выйти.

Вот тут, например. Серое ребро выброшено, а на других еще придется добавлять слишком хитро точки.

Вот тут, например. Серое ребро выброшено, а на других еще придется добавлять слишком хитро точки.
очень простой случай. В пространстве результатов эксперимента ввести расстояние можно - а точки пересечения уже нет. Так что и думать нечегозаставил задуматься
Ну это специальный пример, я думаю в обычной R^2.
Вот тут, например. Серое ребро выброшено, а на других еще придется добавлять слишком хитро точки.В твоём примере минимаксное условие не соблюдено. У меня есть подозрение, что оно может повлиять на наличие пересекающихся рёбер. Поэтому я и написал, что они "могут" быть. Иначе бы не могли, а точно были бы.

А нет, вру. Ты прав. Эти длинные рёбра всё же могут появиться, т.к. в другом месте могут быть большие расстояния между точками. Значит пересекающиеся будут. 

http://ubicomp.algoritmi.uminho.pt/local/concavehull.html
Делаются такие штуки, скорее всего, на основе диаграмм Вороного.
Для точек это должно быть не очень сложно.
Делаются такие штуки, скорее всего, на основе диаграмм Вороного.
Для точек это должно быть не очень сложно.
Вот тут, например. Серое ребро выброшено, а на других еще придется добавлять слишком хитро точки.Подумал.

На самом деле там всё относительно просто с пересечениями должно быть. Просто берём 4 точки, которые образуют рёбра с пересечениями, получим четырёхугольник.
Он либо прямоугольник, тогда точно можно заменть плохие ребра более коротким прямым стыком. Либо один из углов тупой у него, тогда тоже можно тоже более короткими заменить либо прямым стыком оба плохих либо 2 рёбрами одно из плохих.
Короче, мне действительно подошла модификация метода Джарвиса.
Суть в том, что сначала выбмрается нижняя левая точка - считаем, что она всегда принадлежит многоугольнику. Затем беру нитку ограниченной длины (например, 1 один конец привязываю к первой точке. Затем нитку вращаю против часовой стрелки, пока не наткнется на какую-то точку. Беру новую нитку ограниченной длины, привязываю ее ко второй точке. Продолжаю вращать ее против часовой стрелки, начиная от луча, исходящего из первой точки во вторую, пока не найдется третья точка. И т.д.
Если на каком-то шаге алгоритма не найдется точка - то алгортим завершен. Затем для полученного многоугольника проверяется, что все остальные точки лежат внутри него. Если есть такая, что не лежит в нем, то увеличиваем длину нитки (например, умножаем на 2) и все заново, пока не получится многоугольник, содержащий все остальные точки.
То есть, алгорит в отличие от алгоритма Джарвиса имеет параметр - "рекомендуемое" ограничение сверху каждого ребра. Если нельзя найти многоугольник с такими ребрами, то увеличиваем рекомендациию. Метод будет нормально работать для плотно расположенных точек типа , а для редко расположенных будет скорее всего совпадать с выпуклой оболочкой (или незначительно отличаться от нее)
PS. Область действительно предполагается как связной, так и односвязной, т.е. предполагается, что есть многоугольник, который ее хорошо описывает.
Суть в том, что сначала выбмрается нижняя левая точка - считаем, что она всегда принадлежит многоугольнику. Затем беру нитку ограниченной длины (например, 1 один конец привязываю к первой точке. Затем нитку вращаю против часовой стрелки, пока не наткнется на какую-то точку. Беру новую нитку ограниченной длины, привязываю ее ко второй точке. Продолжаю вращать ее против часовой стрелки, начиная от луча, исходящего из первой точки во вторую, пока не найдется третья точка. И т.д.
Если на каком-то шаге алгоритма не найдется точка - то алгортим завершен. Затем для полученного многоугольника проверяется, что все остальные точки лежат внутри него. Если есть такая, что не лежит в нем, то увеличиваем длину нитки (например, умножаем на 2) и все заново, пока не получится многоугольник, содержащий все остальные точки.
То есть, алгорит в отличие от алгоритма Джарвиса имеет параметр - "рекомендуемое" ограничение сверху каждого ребра. Если нельзя найти многоугольник с такими ребрами, то увеличиваем рекомендациию. Метод будет нормально работать для плотно расположенных точек типа , а для редко расположенных будет скорее всего совпадать с выпуклой оболочкой (или незначительно отличаться от нее)
PS. Область действительно предполагается как связной, так и односвязной, т.е. предполагается, что есть многоугольник, который ее хорошо описывает.
Возможно оболочка с минимальной максимальной длиной ребра ему подойдёт.
Да, такое вроде тоже подойдет. Я ошибаюсь или оно будет давать примерно такие же результаты, как и модификация метода Джарвиса?
http://ubicomp.algoritmi.uminho.pt/local/concavehull.htmlДелаются такие штуки, скорее всего, на основе диаграмм Вороного.Для точек это должно быть не очень сложно.Было бы вообще шикарно, правда, хз, как реализовывать:)
Да, такое вроде тоже подойдет. Я ошибаюсь или оно будет давать примерно такие же результаты, как и модификация метода Джарвиса?Ну да, метод Джарвиса как раз строит оболочку с ребром не больше заданной величины. В идеальном случае тебе нужна минимальная такая длина при которой оболочка существует.
Но как я говорил — это суть. А алгоритмы могуть быть разные. Вот метод Джарвиса один из них, мы тут с графом ещё что-то предложить пытались. Возможно диаграммы Вороного что-то подобное тоже, но я не изучал этот вопрос.
Вопрос в том, как правильно найти баланс между расстоянием и выпуклостью.Предлагаю ебанутый функционал, типа, некая монотонная функция от числа вершин (или длины) ломаной + сумма квадратов расстояний до нее всех точек из множества.
Есть идея разбить всю поверхность на квадратики и посмотреть, в какие квадартики попадают точки. а в какие нет. Тогда если правильно выбрать размер квадаратиков, то получится "оценить" площадь.
Размер квадрата можно взять как максимальное из всех минимальных расстояний до соседних точек для каждой точки.
работает при достаточной плотности точек, плюс не потребуется считать площадь многоугольника)
Размер квадрата можно взять как максимальное из всех минимальных расстояний до соседних точек для каждой точки.
работает при достаточной плотности точек, плюс не потребуется считать площадь многоугольника)
Оставить комментарий
onyxis
На плоскости находится какое-то число точек. Нужно найти такой многоугольник, вершинами которого являются точки из этого множества и который содержит внутри себя все остальные точки этого множества.Пример задачи:
Желаемое решение:
Кроме прямого перебора, ничего придумать не могу.Как такую задачу решает человек, внятно объяснить тоже не могу.