[алгоритмическая задача] подсчитать количество достижимых вершин
рёбер у вершины сколько бывает?
я правильно понимаю, что тебе подойдёт поиск в ширину?
если граф сильно связный (со множеством сильно связных компонент то это же вообще довольно много данных.
я правильно понимаю, что тебе подойдёт поиск в ширину?
если граф сильно связный (со множеством сильно связных компонент то это же вообще довольно много данных.
В каком виде хранится граф?
Для начала выдели сильно связные компоненты (за линейное от числа вершин и рёбер время, если не ошибаюсь).
Засчёт этого можно (если повезёт) ощутимо уменьшить размер задачи, и рассматривать только даги.
Засчёт этого можно (если повезёт) ощутимо уменьшить размер задачи, и рассматривать только даги.
рёбер у вершины сколько бывает?Исходящих - от 0 до нескольких десятков. С поиском в ширину - там ведь могут быть циклы, так что не получится учесть, считали мы уже текущую вершину или нет.
В каком виде хранится граф?Специальные внутренние форматы. Или я не понял вопрос?
1. Построить фактор-граф по отношению эквивалентности - вхождение в одну компонент сильно-связности. Сложность O(V+E). Результатом является ациклический ориентированный граф, вершины которого соответствуют компонентам сильно-связности исходного графа.
2. Начиная с "листовых" компонент для каждой вершины суммируем кол-во вершин в содержащей ее компоненте, а также в тех компонентах, которые достижимы из данной. Сложность O(V + N^2 где N - число компонент связности.
2. Начиная с "листовых" компонент для каждой вершины суммируем кол-во вершин в содержащей ее компоненте, а также в тех компонентах, которые достижимы из данной. Сложность O(V + N^2 где N - число компонент связности.
Спасибо =)
А как избежать повторного суммирования (как в случае с ромбом например)?
Мне кажется, можно сделать что-то на основе алгоритма поиска сильно связных компонент. Параллельно с поиском ССК можно строить конденсацию графа, и потом проходом в ширину найти искомое число достижимых вершин (оно будет одинаковым для всех вершин одной СКК). Вроде бы это даже можно скомбинировать в одном цикле и конденсацию явно в виде отдельного графа не строить.
Опоздал
Опоздал

Каждой компоненте присваивается целое число - количество вершин, достижимых из вершин этой компоненты. Так вот начиная с листовых компонент можно избежать необходимости повторного суммирования.
Что должно произойти в таком случае?
http://en.wikipedia.org/wiki/File:Diamond_inheritance.svg
http://en.wikipedia.org/wiki/File:Diamond_inheritance.svg
Здесь была лажа 
Пусть F(X) - вычисление результата для вершин из множества X
F(A) = |A|
F(B) = |B| + F(A)
F(C) = |C| + F(A)
F(D) = |D| + F(B) + F(C)
Для каждого из множеств A, B, C, D функция F вычисляется ровно 1 раз.

F(A) = |A|
F(B) = |B| + F(A)
F(C) = |C| + F(A)
F(D) = |D| + F(B) + F(C)
Для каждого из множеств A, B, C, D функция F вычисляется ровно 1 раз.
Неправильно вычисляется, у тебя получится F(D) = |D|+|B|+|C|+2|A|.
Как сделать правильно без хранения списка всех компонент, которые "ниже", хз.
да, тут я ступил 

О, можно сделать транзитивное замыкание, но вроде это не быстро.
Задача: для каждой вершины произвольного ориентированного графа подсчитать количество достижимых из неё вершин. Размеры графов - от десятков тысяч до миллионов вершин, так что оптимизация по скорости критична. Куда копать?Начинать надо с формата, в котором задан граф.
Как и где он хранится. В памяти? На диске? Может он настолько увесистый, что память лопнет...
Тогда вместо хранения целого числа для каждой компоненты надо хранить список идентификаторов включенных компонент связности. Тогда оценка сложности будет O(V + E + n^2 где n - число компонент связности.
Как и где он хранится. В памяти? На диске? Может он настолько увесистый, что память лопнет..Он вполне себе увесистый (от сотен мегабайт до нескольких гигабайт). В памяти хранится, насколько понимаю, в каждый момент лишь некоторая часть графа.
Как сделать правильно без хранения списка всех компонент, которые "ниже", хздля нескольких миллионов это, возможно, и не нужно
конкретно под эту задачу можно граф хранить в в векторе и к вершинам обращаться по номеру (индексу в массиве)
выделение связных компонент точно нужно? не достаточно ли начинать обходы с вершин, в которые не входит ни одного ребра?
Сейчас попробую нарисовать примерный вид наиболее часто встречающейся конструкции графа (эти самые ромбы)
выделение связных компонент точно нужно? не достаточно ли начинать обходы с вершин, в которые не входит ни одного ребра?Таких может не быть вообще.
Тогда вместо хранения целого числа для каждой компоненты надо хранить список идентификаторов включенных компонент связности. Тогда оценка сложности будет O(V + E + n^2 где n - число компонент связности.Ну да, это по сути транзитивное замыкание и есть.
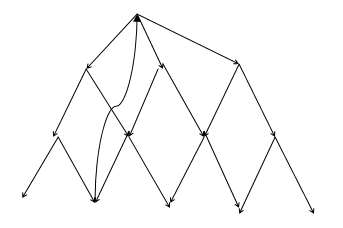
тут цикл
как себя должен вести алгоритм? для участников цикла прописать infinity ?
как себя должен вести алгоритм? для участников цикла прописать infinity ?
тут циклкак себя должен вести алгоритм? для участников цикла прописать infinity ?Прочитай внимательно цель алгоритма: не вычислить длину пути, а посчитать количество достижимых вершин. Бесконечности не будет никогда - из любой вершины достижимо строго меньше V (если не считать себя).
спасибо, понял теперь=)
Такая задача возникает при подсчёте Retained Size объектов для профилирощиков памяти. И она там как-то фигово решена.
Так что, может быть у тебя все-таки не общая постановка для произвольного графа и можно поискать специальный алгоритм?
Так что, может быть у тебя все-таки не общая постановка для произвольного графа и можно поискать специальный алгоритм?Я нарисовал примерный вид графа. Вот такой ромбовой структуры может быть несколько сотен этажей, постоянно расширяющихся, и иногда встречаются пути куда-нибудь наверх или в сторону.
а "вершины" всех пирамид как-нибудь можно быстро запросить? или дополнительной информации нет?
Ну ты мог бы формально описать, какого и только какого вида может быть граф?
Ну тогда копец 
То есть для десятка тысяч вершин может еще и получится что-то сделать, но не для миллиона уж точно.
А что реально нужны эти миллион значений (для каждой вершины) одновременно? Просто если они, к примеру, нужны одна за другой по очереди, то эту задачу уже вполне можно решить за разумное для одной итерации время.

То есть для десятка тысяч вершин может еще и получится что-то сделать, но не для миллиона уж точно.
А что реально нужны эти миллион значений (для каждой вершины) одновременно? Просто если они, к примеру, нужны одна за другой по очереди, то эту задачу уже вполне можно решить за разумное для одной итерации время.
Одновременно, конечно же, не нужно. Надо просто за разумное время вычислить эту величину для каждой вершины и приписать к ней.
а "вершины" всех пирамид как-нибудь можно быстро запросить? или дополнительной информации нет?Если под "вершиной пирамиды" подразумевать вершину графа, в которую не входит ни одного ребра, то - нет (скорее всего в каждую вершину входит как минимум одно ребро).
Ну ты мог бы формально описать, какого и только какого вида может быть граф?Ограничений практически нет. Точно не может быть циклов четной длины (в частности, если есть переход a->b, то перехода b->a нет). Если придумаю что-то еще, скажу.
Пример графа есть? Можешь выложить в текстовом формате, где каждая строчка описывает ребро между двумя вершинами. Что-то типа:
Тогда можно было бы посмотреть на граф и померяться реализациями алгоритмов. По-моему, вышло бы прикольно.
1 2
2 3
4 3
Тогда можно было бы посмотреть на граф и померяться реализациями алгоритмов. По-моему, вышло бы прикольно.
Для того, чтобы меряться реализациями алгоритма надо сначала определить сам алгоритм. Меряться реализациями разных алгоритмов имеет смысл только когда нет другого способа сравнения этих алгоритмов (а в данном случае это не так). Это как сравнивать реализацию сортировки пузырьком с реализацией сортировки кучей — алгоритмы имеют разные свойства. Качество алгоритма (и, соответственно, ценность полученного результата) определяется в первую очередь его теоретическими свойствами, а не тем, насколько хорошо он закодирован в виде реализации. Итак, какова асимптотическая сложность твоего алгоритма?
Сначала ты предлагаешь разбивать на сильно связные компоненты и выдаешь это за решение, хотя никто не говорил, что эти компоненты большие и это сильно упростит задачу. Теперь вот ты говоришь, реализации сравнивать бессмысленно (а это как раз очень осмысленно).
Хватит теоретизировать.
Да, пускай GDM выложит графы. Пусть скажет, что это полный набор тестов. Тогда я тоже возьмусь попишу, давно ничего не кодил подобного
Хватит теоретизировать.
Да, пускай GDM выложит графы. Пусть скажет, что это полный набор тестов. Тогда я тоже возьмусь попишу, давно ничего не кодил подобного

Ну вот, кстати, о сортировках и их реализациях. Недавно проспорил другу пивасик, не смог написать qsort, который работает быстрее вставок на случайном массиве длины 100. Хотя оптимизации он мне разрешил юзать разные, например, короткие массивы (до 8ми) я сортировал его же функцией 

В треде спрашивается про алгоритм, а не про его реализацию. В результате сравнения реализаций алгоритма можно получить разве что стандартную таблицу значений - параметры входных данных - параметры выходных данных. И какие же выводы это позволит сделать в отношении алгоритмов?
Ну алгоритмы же мы тоже опишем. И оптимизации.
Ну вот, кстати, о сортировках и их реализациях. Недавно проспорил другу пивасик, не смог написать qsort, который работает быстрее вставок на случайном массиве длины 100. Хотя оптимизации он мне разрешил юзать разные, например, короткие массивы (до 8ми) я сортировал его же функциейЭто как раз то, о чем я и говорил. Случайная реализация алгоритма не позволяет судить о самих алгоритмах. То, что предлагается меряться скоростью - это чистой воды задротство.
Ты неправ. Это не задротство, а напротив, некоторая программистская мудрость. Вот как в соседнем треде обсуждают про printf vs stringstreams, так и здесь: если массив маленький, то писать асимптотически пиздатый qsort не надо.
Сначала ты предлагаешь разбивать на сильно связные компоненты и выдаешь это за решение, хотя никто не говорил, что эти компоненты большие и это сильно упростит задачу.Во-первых, поскольку сложность операции линейная, это задачу точно не усложнит. А значит, это целесообразно. Во-вторых, это сразу позволяет свести задачу для произвольного графа к задаче для ациклического графа. Ну а в-третьих, пока еще никто в данном треде не предложил лучшего алгоритма.
В данном случае (несколько миллионов вершин) играет роль именно асимптотическая сложность задачи.
Ну неправда это. Никогда не влияет «только асимптотическая сложность». Нету у нас бесконечностей, нету. Асимптотика — это просто подсказка, как не считая все точно прикинуть время работы.
Если алгоритм линейный, то разбиение на компоненты связности может замедлить работу в полтора-два раза. В зависимости от линейности двух частей алгоритма.
Ладно, я начинаю думать и писать, ты бы тоже написал, полезно будет.
Ладно, я начинаю думать и писать, ты бы тоже написал, полезно будет.
Во-вторых, это сразу позволяет свести задачу для произвольного графа к задаче для ациклического графаЭто аргумент (пока индуктивный). Все остальное — нет.
Первое и третье утверждения относятся вот к чему:
Сначала ты предлагаешь разбивать на сильно связные компоненты и выдаешь это за решение, хотя никто не говорил, что эти компоненты большие и это сильно упростит задачу.Решение было приведено ранее, вопрос в том, насколько оно хорошее. А разбиение на компоненты лишь потенциально может усложнить задачу в 2 раза, и только в том случае, если кто-то предложит линейный алгоритм, не использующий это разбиение. А этого пока никто не сделал.
Ладно, я начинаю думать и писать, ты бы тоже написал, полезно будет.Предлагаю подумать, какова была бы сложность решения задачи, если изначально было бы известно, что граф ациклический. Ясно, что сложность решения для произвольного графа не меньше сложности решения для ациклического. А тут, мне кажется, все плохо. Не получается придумать линейный алгоритм, а только квадратичный. Если вершин у нас порядка 10^6, то операций будет порядка 10^12.
Не получается придумать линейный алгоритм, а только квадратичный.Квадратичный алгоритм можно написать без заморочек: для каждой вершины делаем полный обход графа, выставляя флажки, и всё.
В общем случае решать неинтересно и лениво (но я попробую все равно, пусть будет).
Все-таки ты пояснишь, что там с двудольностью, циклами? Скажи уже все, что о нем знаешь наверняка.
Все-таки ты пояснишь, что там с двудольностью, циклами? Скажи уже все, что о нем знаешь наверняка.
Да, но такой алгоритм квадратичен всегда (сложность - "тета от N" где N - число вершин.
А заморочки позволяют его сделать квадратичным лишь в самых плохих случаях.
А заморочки позволяют его сделать квадратичным лишь в самых плохих случаях.
Это ты сказал V * (V + E это чуть хуже, чем просто квадратично.
А, ну кстати там, насколько я понимаю V почти равно E, даже не в два раза отличие. вот это странно.
Или там у тебя номера вершин как-то сильно раскиданы?
Или там у тебя номера вершин как-то сильно раскиданы?
Например, можно считать, что сложность алгоритма O(E + V*N где N - максимальное число "родителей" вершины ациклического графа. Например, если N = log V, то квадратичности может и не быть. В случае с ромбами, N будет порядка V (для листовых вершин и суммарная сложность O(E + V^2).
в чем кстати смысл ребер в самих себя?
в чем кстати смысл ребер в самих себя?А такие есть? Вообще-то не должно быть. Граф совершенно точно двудольный. Про циклы четной длины - мой косяк, конечно же. Циклы могут быть. V примерно равно E, тоже правда.
А такие есть? Вообще-то не должно быть. Граф совершенно точно двудольный. Про циклы четной длины - мой косяк, конечно же. Циклы могут быть. V примерно равно E, тоже правда.первая же строчка
00000002 00000002
Ну скажи, что за графы, пожалуйста! У тебя же нарисован непростой граф, там треугольник такой длинный. Где там двудольность, тоже не совсем понятно.
Ладно, граф двудольный. Т.е. постановка такая: в двудольном графе тарам пам-пам, так?
В общем виде действительно ничего хорошего не выйдет походу.
Ладно, граф двудольный. Т.е. постановка такая: в двудольном графе тарам пам-пам, так?
В общем виде действительно ничего хорошего не выйдет походу.
В общем виде действительно ничего хорошего не выйдет походу.его пример халявным алгоритмом где-то за минуту обсчитывается
Ладно, может быть, но это не круто.
Ну скажи, что за графы, пожалуйста! У тебя же нарисован непростой граф, там треугольник такой длинный. Где там двудольность, тоже не совсем понятно.Открою секрет, что уж там

Вершины - шахматные позиции (позиция = расстановка фигур+флаги рокировок и взятий на проходе+чей ход). Дуги - шахматные ходы.
Двудольность очевидна?

P.S. Задачка не модельная, и мне тоже интересно, есть ли неквадратичное решение.
отличчно. Так бы сразу 

Кстати, циклы четной длины быть там могут. Нечетной не могут. Ну это из двудольности следует.
И еще добавка. Как правильно заметил , вычислять значение для всех вершин не обязательно. В каждый момент нужна только информация по порядка 20 вершин (всех, инцидентных одной данной но мгновенно.
Если считать их просто в виде 20 поисков, скажем, в глубину, то это займет неприемлимо большое время.
Т.е. надо либо посчитать сразу для всех V вершин за меньшее, чем V^2 время (я тут предполагаю, что V и E одного порядка либо за это же время построить структуру, которая поможет считать значение для одной вершины быстрее, чем за V.
P.S. Я сомневаюсь, что на этом графе вообще возможен поиск в ширину: может не хватить памяти под очередь вершин.
Если считать их просто в виде 20 поисков, скажем, в глубину, то это займет неприемлимо большое время.
Т.е. надо либо посчитать сразу для всех V вершин за меньшее, чем V^2 время (я тут предполагаю, что V и E одного порядка либо за это же время построить структуру, которая поможет считать значение для одной вершины быстрее, чем за V.
P.S. Я сомневаюсь, что на этом графе вообще возможен поиск в ширину: может не хватить памяти под очередь вершин.
надо уже убегать, но на 2/3 реализовал следующий алгоритм
вначале убираем циклы, стягивая их в точку, следующим образом
итерационно
последовательно обрубаем одиноких родителей и детей (которые явно невходят в циклы)
берем первый попавшийся путь - как только он заворачивается в цикл (а это обязательно произойдет,
т.к. все тупики уже выкинули) его заменяем на точку
в итоге, получили граф без циклов, но с точками разной мощности.
запускаем подсчет результата.
первая половина, халявно написанная, отрабатывает на примере секунд за 40
вторую - подсчет по графу без циклов - еще не реализовал
вначале убираем циклы, стягивая их в точку, следующим образом
итерационно
последовательно обрубаем одиноких родителей и детей (которые явно невходят в циклы)
берем первый попавшийся путь - как только он заворачивается в цикл (а это обязательно произойдет,
т.к. все тупики уже выкинули) его заменяем на точку
в итоге, получили граф без циклов, но с точками разной мощности.
запускаем подсчет результата.
первая половина, халявно написанная, отрабатывает на примере секунд за 40
вторую - подсчет по графу без циклов - еще не реализовал
P.S. Я сомневаюсь, что на этом графе вообще возможен поиск в ширину: может не хватить памяти под очередь вершин.в примере, ребер порядка 200к - это 1мб памяти
Я говорил не о примере, а об общем случае.
Вообще, мне кажется, что найденное здесь решение далеко не факт, что окажется применимым, т.к. GDM не хочет описывать структуру данных, в которой хранится граф.
Например, твой алгоритм стягивания циклов подразумевает удаление вершин и добавление новых "фиктивных" вершин. Исходная структура данных для хранения графа не умеет хранить произвольные новые вершины.
Вообще, мне кажется, что найденное здесь решение далеко не факт, что окажется применимым, т.к. GDM не хочет описывать структуру данных, в которой хранится граф.
Например, твой алгоритм стягивания циклов подразумевает удаление вершин и добавление новых "фиктивных" вершин. Исходная структура данных для хранения графа не умеет хранить произвольные новые вершины.
Исходная структура данных для хранения графа не умеет хранить произвольные новые вершины.зачем это хранить в самом графе? почему это нельзя хранить снаружи?
можно. Но их количество может оказаться сравнимо с V. Тогда придется придумать хороший формат для хранения, с откачкой на диск.
можно. Но их количество может оказаться сравнимо с V. Тогда придется придумать хороший формат для хранения, с откачкой на диск.какой диск?

Размеры графов - от десятков тысяч до миллионов вершин
Исходящих - от 0 до нескольких десятков.это даже по максимуму в 0.5гб памяти влазит
Я, возможно, не врубился в суть твоего удаления циклов, но мне кажется, что условие "Исходящих - от 0 до нескольких десятков" перестанет выполняться для фиктивных вершин в процессе счета.
Я, возможно, не врубился в суть твоего удаления циклов, но мне кажется, что условие "Исходящих - от 0 до нескольких десятков" перестанет выполняться для фиктивных вершин в процессе счета.общее кол-во ребер: "несколько млн * несколько десятков исходящих" будет лишь уменьшаться при стягивании циклов в точку.
т.е. ты предлагаешь поместить весь граф в память, пронумеровав вершины, и произвести подсчет в памяти. Правильно?
Насколько я понимаю, твой алгоритм избавления от циклов является на самом деле алгоритмом поиска (и стягивания в одну точку) сильно связных компонент. После чего задача сводится к задаче над ациклическим графом.
Решения задачи с ацикличесмким графом пока еще не предлагали, верно?
Насколько я понимаю, твой алгоритм избавления от циклов является на самом деле алгоритмом поиска (и стягивания в одну точку) сильно связных компонент. После чего задача сводится к задаче над ациклическим графом.
Решения задачи с ацикличесмким графом пока еще не предлагали, верно?
т.е. ты предлагаешь поместить весь граф в память, пронумеровав вершины, и произвести подсчет в памяти. Правильно?да
Насколько я понимаю, твой алгоритм избавления от циклов является на самом деле алгоритмом поиска (и стягивания в одну точку) сильно связных компонент. После чего задача сводится к задаче над ациклическим графом.да
Решения задачи с ацикличесмким графом пока еще не предлагали, верно?предлагали, но не линейное
предлагали, но не линейноеПредлагали квадратичное, а это асимптотически не лучше straightforward решения с V обходами в глубину. Поэтому я его за решение не считаю

Предлагали квадратичное, а это асимптотически не лучше straightforward решения с V обходами в глубину. Поэтому я его за решение не считаювертится мысль, что от слипаний тоже можно избавиться через выделение "циклов" и замену их на "кляксы".
но нужно время поковыряться.
первая половина, халявно написанная, отрабатывает на примере секунд за 40Это обсчёт для одной вершины или для всех? Пример, который я кинул - самое маленькое дерево из имеющихся под рукой. Остальные до 1000 раз больше.
PS Генератор примеров накосячил, ребер самих в себя быть точно не должно. Баг найду и поправлю, но позже.
Это обсчёт для одной вершины или для всех?для всех конечно.
В этом примере граф ещё и не двудольный
В этом примере граф ещё и не двудольныйТочно генератор кривой
 Зарекусь писать спросонья..
Зарекусь писать спросонья..Оставить комментарий
Dimon89
Задача: для каждой вершины произвольного ориентированного графа подсчитать количество достижимых из неё вершин. Размеры графов - от десятков тысяч до миллионов вершин, так что оптимизация по скорости критична. Куда копать?