Построить контур, содеражщий данные окружности.
сразу возникают вопросы:
1) внешний контур произвольный или выпуклый?
2) > окружностей, которые могут касаться границ контура или дырок, но не пресекают их.
могут касаться или обязаны касаться?
3) имхо не очевидно, что существует единственный контур удовлетворяющий условиям - соответственно либо условие надо усилять либо говорить что любой подойдет
ЗЫ хотя на счет 3-го я неуверен - может и очевидно что он единственный - лень под вечер думать )
ЗЗЫ навскидку кажется что надо построить оболочку всех окружностей без учета дырок и потом смотреть с какими дырками она пересекается (это для выпуклого контура - в невыпуклого надо додумать мальца - можно эмулировать "впуклости" дырками) туплю
1) внешний контур произвольный или выпуклый?
2) > окружностей, которые могут касаться границ контура или дырок, но не пресекают их.
могут касаться или обязаны касаться?
3) имхо не очевидно, что существует единственный контур удовлетворяющий условиям - соответственно либо условие надо усилять либо говорить что любой подойдет
ЗЫ хотя на счет 3-го я неуверен - может и очевидно что он единственный - лень под вечер думать )
3) Является минимальным, то есть не содержит других контуров, удовлетворяющих 1) и 2) .это неоднозначно, ты ведь в курсе. Любого достаточно, не обязательно минимальный по периметру, скажем?
ЗЫ хотя на счет 3-го я неуверен - может и очевидно что он единственный - лень под вечер думать )представь три окружности для определенности с центрами в вершинах равностороннего треугольника и "дырка" посередине этого треугльника. "Обходить" ее можно разными способами.
зачем ее вообще обходить? вроде не сказано ведь, что внутри искомого контура не должно быть дырок?
А дырки между собой могут пересекаться? Понятно, что это несущественно, просто любопытно.
и могут ли дырки касаться границ внешнего контура (хз, правда, важно ли это)
в общем про выпуклость контура/дырок интересно узнать. Ну и можно саму задачу, откуда это вылезло - просто интереса ради
в общем про выпуклость контура/дырок интересно узнать. Ну и можно саму задачу, откуда это вылезло - просто интереса ради
Выпуклость необязательна.
Окружности обязательно касаются внешнего контура и имеют по крайней мере еще одну точку касания (внешнего контура лии дырки но это не важно на мой взгляд.
Про условие 3 подойдет любой. Хотя учитывая, откуда берется задача, то скорее всего будет единственность.
В результирующем контуре не должно быть дырок.
Окружности обязательно касаются внешнего контура и имеют по крайней мере еще одну точку касания (внешнего контура лии дырки но это не важно на мой взгляд.
Про условие 3 подойдет любой. Хотя учитывая, откуда берется задача, то скорее всего будет единственность.
В результирующем контуре не должно быть дырок.
В результирующем контуре не должно быть дырок.Тогда мой пример с небольшими модификациями испортит единственность. Просто мне сразу показалось, что не зря эти объекты названы именно дырками

Если без дырок, то решение элементарное:
Проходим точки касания по часовой стрелке. Если две соседние точки касания принадлежат одной окружности, то соединяем их дугой этой окружности, если разным - то куском контура.
Проходим точки касания по часовой стрелке. Если две соседние точки касания принадлежат одной окружности, то соединяем их дугой этой окружности, если разным - то куском контура.
Если в твоем примере дырка не касается окружностей, то контур без этой дырки вообще нельзя построить. А если касается, то как и каких?
я бы переформулировала на языке графов, чтобы геометрию всю выкинуть, только топологию оставить
окружности - ориентированные ребра графа
дырки - те же окружности, но ориентированные в противоположную сторону
окружности - ориентированные ребра графа
дырки - те же окружности, но ориентированные в противоположную сторону
Всех касающаяся дырка. Или цикл должен быть простым, а не только без самоналожений?
Не понял вопроса.
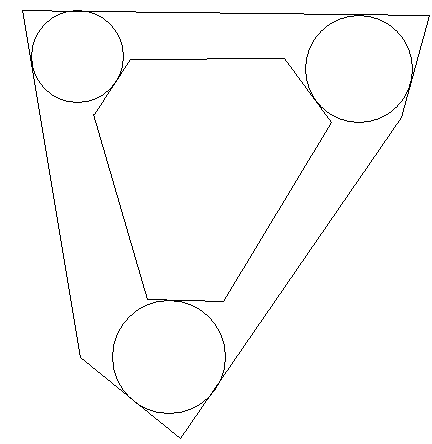
вот, в этом случае 3 (три) минимальных по включению контура есть.
Что конкретно не понятно, понятие "простой цикл"?
В любом случае, это все равно лишнее, зря я этот вопрос задал.
В любом случае, это все равно лишнее, зря я этот вопрос задал.
Точнее, минимальных. Да, три. Подходит любой.
Оставить комментарий
Devid
Дано:Замкнутый контур (из отрезков и дуг с несколькими дырками (тоже из отрезков и дуг). Кроме того несколько окружностей, которые могут касаться границ контура или дырок, но не пресекают их.
Надо:
Построить замкнутый контур, который:
1) Содержит все окружности.
2) Состоит из кусков исходного контура и контуров дырок и дуг данных окружностей.
3) Является минимальным, то есть не содержит других контуров, удовлетворяющих 1) и 2) .
Пример (внутри треугольная дырка, красное - результат):