Анализ форм: найти длину фигуры и ширину ее самого тонкого места
Что подразумевается под длиной фигуры, например, сосиски?
может, максимальный отрезок, который можно впихнуть в эту сосиску
Можно построить диаграмму Вороного, в ней есть информация о "ширине". Хотя это достаточно сложно.
Если длина - это расстрояние между самыми дальними точками, то можно попробовать вписать в окружность каким-либо образом.
Узкое место можно попробовать найти "расширяя" контур пока не появится пересечение. Но тут не очень очевидно, т.к. если 2 недалёкие точки вдоль одной стороны контура взять, то это как бы тоже за узкое место можно считать. Т.е. нужно как-то формализовать это понятие более "надёжно".
Узкое место можно попробовать найти "расширяя" контур пока не появится пересечение. Но тут не очень очевидно, т.к. если 2 недалёкие точки вдоль одной стороны контура взять, то это как бы тоже за узкое место можно считать. Т.е. нужно как-то формализовать это понятие более "надёжно".
Для выпуклой фигуры хорошо думаю сработает:
1. Выделить гантелю как связную область.
2. Найти ориентацию связной области(Что это такое хорошо описано в лекциях по машграфу ВМК 2ой курс. Или гуглить по словам: ось минимального второго момента.)
3. Через центр масс фигуры(см те же лекции или инет
) провести ось ориентации. Длина фигуры - это длина отрезка построенной оси, заключенной внутри фигуры. Ширина самого узкого места - минимальная длина отрезка, заключенного внутри фигуры и перпендикулярного построенной оси.
1. Выделить гантелю как связную область.
2. Найти ориентацию связной области(Что это такое хорошо описано в лекциях по машграфу ВМК 2ой курс. Или гуглить по словам: ось минимального второго момента.)
3. Через центр масс фигуры(см те же лекции или инет
) провести ось ориентации. Длина фигуры - это длина отрезка построенной оси, заключенной внутри фигуры. Ширина самого узкого места - минимальная длина отрезка, заключенного внутри фигуры и перпендикулярного построенной оси.Если длина - это расстрояние между самыми дальними точками, то можно попробовать вписать в окружность каким-либо образом.Что-то я не понял, если длина — это расстояние между самыми дальними точками, то если известна граница, оно несложно ищется, даже есть эффективные алгоритмы за N log N. Можно прочитать, например, в Кормене.
Про ширину эффективного алгоритма не знаю, но помню на втором курсе писал одному парню из чего-то авиационного программку для расчета каких-то параметров крыла, там как раз была фигура в форме сосиски и надо было найти ГМТ точек-центров окруженостей, которые касаются ее контура в двух точках.
Можно сделать подобным образом. Т.е. обходить границу, по некоторой окрестности прикидывать производную в данном месте, потом методом деления пополам раздувать окружность, которая касается контура в данной точке пока в нее не попадет заметно удаленная точка контура (это чтобы исключить всякие глюки, когда захватываются соседние точки). Вроде бы если перебрать эти окружности, то самое узкое место будет совпадать с локальными минимума диаметров этих окружностей. Но надо немного доработать (там как раз в углах сосиски не совсем понятные вещи происходят).
Можно сделать подобным образом. Т.е. обходить границу, по некоторой окрестности прикидывать производную в данном месте, потом методом деления пополам раздувать окружность, которая касается контура в данной точке пока в нее не попадет заметно удаленная точка контура (это чтобы исключить всякие глюки, когда захватываются соседние точки). Вроде бы если перебрать эти окружности, то самое узкое место будет совпадать с локальными минимума диаметров этих окружностей. Но надо немного доработать (там как раз в углах сосиски не совсем понятные вещи происходят).
Спасибо за советы, буду обдумывать.
Что такое длина: понятия не имею, как ее формализовать. Если б знал — было бы проще. Однако большинство людей однозначно ее бы определили на глаз — значит, это объективная величина, и какое-то определение у нее должно быть.
Нет, длина фигуры — это не расстояние между самыми дальними точками (диаметр) и не длина отрезка. Если прямую сосиску согнуть в подкову, диаметр и макс. хорда уменьшатся, а длина сохранится. Фиг знает, как определить такую длину. Может, подкажете?
Что такое длина: понятия не имею, как ее формализовать. Если б знал — было бы проще. Однако большинство людей однозначно ее бы определили на глаз — значит, это объективная величина, и какое-то определение у нее должно быть.
Нет, длина фигуры — это не расстояние между самыми дальними точками (диаметр) и не длина отрезка. Если прямую сосиску согнуть в подкову, диаметр и макс. хорда уменьшатся, а длина сохранится. Фиг знает, как определить такую длину. Может, подкажете?
Предлагаю посмотреть в гугле/википедии ключевые слова "Fast marching method".
С его помощью можно найти длину сосики следующим образом: берём произвольную точку сосиски, и с помощью FSM находим граничную точку, наиболее удалённую от заданной. Теперь начинаем от неё, и находим опять наиболее удалённую. Так до тех пор, пока получающиеся расстояния не перестанут расти. Это мы найдём наибольшее кратчайшее расстояние между парой точек внутри нашей сосиски. Вполне разумно называть это длиной сосиски.
С его помощью можно найти длину сосики следующим образом: берём произвольную точку сосиски, и с помощью FSM находим граничную точку, наиболее удалённую от заданной. Теперь начинаем от неё, и находим опять наиболее удалённую. Так до тех пор, пока получающиеся расстояния не перестанут расти. Это мы найдём наибольшее кратчайшее расстояние между парой точек внутри нашей сосиски. Вполне разумно называть это длиной сосиски.
Разумно, спасибо большое.
Мы что-то такое в школе проходили (называли его "метод волн" для поиска пути в лабиринте только сейчас об этом вспомнил.
Мы что-то такое в школе проходили (называли его "метод волн" для поиска пути в лабиринте только сейчас об этом вспомнил.
Если учесть "ширину самого тонкого места", я бы формализовал "длину" так:
минимальная длина собственной (i. e. состоящей из внутренних и граничных точек) кривой, соединяющей две точки, расстояние между которыми есть диаметр.
минимальная длина собственной (i. e. состоящей из внутренних и граничных точек) кривой, соединяющей две точки, расстояние между которыми есть диаметр.
Эх, трясущиеся мои руки... =)
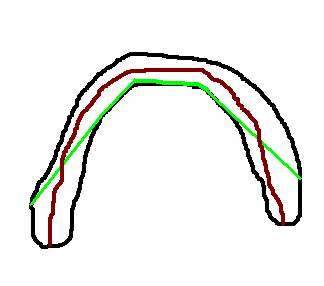
Мне кажется, автору хочется формализовать так, чтобы было ближе к бордовой, чем к салатовой линии.
Это можно сделать для штук, похожих на сосиску, тоже через те окружности, о которых я говорил. Это будет длина того самого ГМТ их центров плюс сумма радиусов граничных окружностей.
Мне кажется, автору хочется формализовать так, чтобы было ближе к бордовой, чем к салатовой линии.
Это можно сделать для штук, похожих на сосиску, тоже через те окружности, о которых я говорил. Это будет длина того самого ГМТ их центров плюс сумма радиусов граничных окружностей.
Ну можно сказать "наибольшая длина выпуклой кривой, целиком состоящей из..." Для фигур небольшой толщины это будет настолько же контринтуитивно.
построй скелет этой своей сосиски.
можно попробовать формализовать длину как наидлиннейший путь в скелете,
а ширину как наибольшее уклонение от скелета.
по-крайней мере, в эту сторону можно подумать.
можно попробовать формализовать длину как наидлиннейший путь в скелете,
а ширину как наибольшее уклонение от скелета.
по-крайней мере, в эту сторону можно подумать.
Я подумал в такую сторону: а если найти диаметр сосиски методом, предложенным выше, взять две наиболее удаленные друг от друга точки и начать "растворять" фигуру послойно. Когда внутрисосисочный путь между этими точками исчезнет — ширина самого тонкого места найдена.
(у предложенного метода поиска длины, кстати, есть незначительный недостаток: если фигура ромб с углом чуть больше 60град, и если стартовать с тупого угла, то метод найдет малую диагональ вместо большой).
(у предложенного метода поиска длины, кстати, есть незначительный недостаток: если фигура ромб с углом чуть больше 60град, и если стартовать с тупого угла, то метод найдет малую диагональ вместо большой).
Оставить комментарий
dimi61
Есть растровая 2d-картинка. Допустим для простоты, что двухцветная, и если надо, то контур ее уже найден.На картинке не очень разветвленная фигура. Ожидается, что это может быть изогнутая сосиска или гантеля неправильной формы, или гантеля с дополнительными узлами типа гирлянды.
Хочется найти длину сосиски-гантели-гирлянды и ширину ее самого узкого места.
Есть ли стандартные способы? Если нет, то подбросьте, пожалуйста, идеи, как считать.
Спасибо.