Помогите найти алгоритм решения задачки
Вырази вектор А'О' через вектора А'В' и А'С'. ( А' В' С' - видимые вершины, О' - видимая точка ). А'О' = а*А'В' + в*А'С'. Затем получи точку К = a*АB + b*AC. Хотя это и неверно в общем случае, но вполне пойдет.
Хотя это и неверно в общем случаеПочему?
Так как это верно если преобразование - афинное(блин, так ли это? Все из головы уже вылетело 
). Если учесть что это не так, да еще если учесть структуру глаза смотрящего(камеры то это очевидно неверно.
). Если учесть что это не так, да еще если учесть структуру глаза смотрящего(камеры то это очевидно неверно.Затем получи точку К = a*АB + b*ACИли уж AК = a*АB + b*AC, или К = a*(А-B) + b*(A-C)
Ну лажно, это и так понятно
Есть чуть более симметричный способ.
По точкам A' B' C' расчитываются так называемые "бариоцентрические коордитаты" (за правописание не ручаюсь) точки O'. Это три числа (a,b,c) со свойствами
1) a+b+c = 1
2) O' = aA' + bB' + cC'
(Я отождествляю точку X с вектором QX, где Q - начало координат, от его выбора ничего не зависит, так что можно считать, что Q = (0,0
Далее вычисляем
O = aA + bB + cC
неверно в общем случаеИмеется в виду, что это построение применимо при параллельном (а не центральном) проектировании. При центральном проектировании (с известным центром) удобно применить те же самые построения в проективном пространстве большей размерности. Но над этим я уже буду напрягаться по отдельной просьбе
по отдельной просьбеЗа сок?
Вообще-то я уже так далек от этого. Надо как-то въехать во все написанное.
Все это нужно для вычисления координат положения животных по фотографиям, которые делались из одного места. Можно определить координаты фотографирующего а также высоту.
Спасибо! Будем подумать.
>Имеется в виду, что это построение применимо при параллельном (а не центральном) проектировании.
R U Sure? Потому что ИМХО и при центральном проектировании это так (ибо описывается линейным оператором (матрицей.
Это может быть неверно если у тебя камера fish eye, но тогда изображение треугольника уже не является треугольником.
R U Sure? Потому что ИМХО и при центральном проектировании это так (ибо описывается линейным оператором (матрицей.
Это может быть неверно если у тебя камера fish eye, но тогда изображение треугольника уже не является треугольником.
центральном проектировании это так (ибо описывается линейным оператором (матрицей.Нет, центральное проектирование не линейное (lol
) хотя бы потому, что оно является преобразованием точек но не векторов (равные векторы могут перейти в неравные, при линейных преобразованиях такого не бывает). Зато центральное проектирование становится линейным при переходе в проективное n+1 мерное пространство и задается соответственно матрицей (n+1)x(n+1)А можно ли как-то определить ошибку такого преоразования
А! Да, конечно... Я уже к этим четырёхмерным векторам так привык, что не замечаю их четырёхмерности нифига =)
2 Алекс2004: Имеется в виду что ты трёхмерные вектора превращаешь в четырёхмерные проективные (x,y,z) -> (x,y,z,1) (обратный переход: (x,y,z,w) -> (x/w, y/w, z/w после чего оператор проектирования представляется в виде матрицы 4х4 (конкретный вид ищешь в любой книжке/доке про программирование 3д графики для начинающих). А дальше, по ходу, делать нужно следующее: умножаешь спроектированный вектор (он при этом тоже должен быть четырёхмерным, кстати) на обратную к ней матрицу, и находишь точку пересечения прямой постороенной на нём как на направляющей с той плоскостью, по которой бегают зверюшки.
Предварительно обязательно нужно найти книжку про программирование 3д и прочитать там теоретические основы.
2 Алекс2004: Имеется в виду что ты трёхмерные вектора превращаешь в четырёхмерные проективные (x,y,z) -> (x,y,z,1) (обратный переход: (x,y,z,w) -> (x/w, y/w, z/w после чего оператор проектирования представляется в виде матрицы 4х4 (конкретный вид ищешь в любой книжке/доке про программирование 3д графики для начинающих). А дальше, по ходу, делать нужно следующее: умножаешь спроектированный вектор (он при этом тоже должен быть четырёхмерным, кстати) на обратную к ней матрицу, и находишь точку пересечения прямой постороенной на нём как на направляющей с той плоскостью, по которой бегают зверюшки.
Предварительно обязательно нужно найти книжку про программирование 3д и прочитать там теоретические основы.
Если не удастся, то я готов за некоторое достаточно большое количество пива (ну... полъящика Жигулёвского!) написать вычислительную часть на С/С++.
Возможно придется обратится за помошью
А сколько в 1/2 ящике бутылок?
А сколько в 1/2 ящике бутылок?
10.
Если решишь - обращайся в аську (174183744).
Если решишь - обращайся в аську (174183744).
В этом семестре я дал такю задачу одному студенту:
Есть триангуляция и значения функции в узлах == множество треугольников в пространстве.
Нужно построить проекцию этого множества на некоторую плоскость, заданную:
1) Точкой, где находится камера (ViewX,ViewY,ViewZ)
2) Направлением, куда камера смотрит (DirX,DirY,DirZ)
3) Направлением, где "верх" у камеры (UpX,UpY,UpZ)
нужно построить треугольники и отсортировать их в порядке удаления от плоскости камеры, нарсовать сначала дальние, потом ближние - получится так, что невидимые линии будут закрашены сами собой.
Данная задача у меня уже реализована, на паскале.
Хочу сказать, что там всё довольно очевидно и самая большая
трудность - это выкладки из аналитической геометрии.
например, если мы знаем, что точка P принадлежит некоторой плоскости, на которой есть базис (u,v задающий лок.координаты и точка O, задающая начало отсчёта, то локальные координаты в плоскости получаются из соотношений:
x_loc=(OP,u);
y_loc=(OP,v); - скалярно умножение трёхмерных векторов.
Найти точку пересечения прямой, соединяющей "точку наблюдения" и одну из вершин имхо довольно просто.
Пусть плоскость (p) задаётся 4 коэффициентами (Ax+By+Cz+D=0 нормаль n = (A,B,C
Луч, с которым надо пересеч плоскость задаётся Ord- начало, Dir - направление.
1) Если S= (Dir, n ) =0, то плоскость и луч параллельны
2) В противном случае считаем точку пересечения:
Dist = -(P.D+(Ord,n/S; // внутренние скобки - скалярное произведение
X = Ord+Dir*Dist
Dist - расстояние от точки Ord до точки X - точки пересечения с плоскостью, измеренное в векторах Dir.
Есть триангуляция и значения функции в узлах == множество треугольников в пространстве.
Нужно построить проекцию этого множества на некоторую плоскость, заданную:
1) Точкой, где находится камера (ViewX,ViewY,ViewZ)
2) Направлением, куда камера смотрит (DirX,DirY,DirZ)
3) Направлением, где "верх" у камеры (UpX,UpY,UpZ)
нужно построить треугольники и отсортировать их в порядке удаления от плоскости камеры, нарсовать сначала дальние, потом ближние - получится так, что невидимые линии будут закрашены сами собой.
Данная задача у меня уже реализована, на паскале.
Хочу сказать, что там всё довольно очевидно и самая большая
трудность - это выкладки из аналитической геометрии.
например, если мы знаем, что точка P принадлежит некоторой плоскости, на которой есть базис (u,v задающий лок.координаты и точка O, задающая начало отсчёта, то локальные координаты в плоскости получаются из соотношений:
x_loc=(OP,u);
y_loc=(OP,v); - скалярно умножение трёхмерных векторов.
Найти точку пересечения прямой, соединяющей "точку наблюдения" и одну из вершин имхо довольно просто.
Пусть плоскость (p) задаётся 4 коэффициентами (Ax+By+Cz+D=0 нормаль n = (A,B,C
Луч, с которым надо пересеч плоскость задаётся Ord- начало, Dir - направление.
1) Если S= (Dir, n ) =0, то плоскость и луч параллельны
2) В противном случае считаем точку пересечения:
Dist = -(P.D+(Ord,n/S; // внутренние скобки - скалярное произведение
X = Ord+Dir*Dist
Dist - расстояние от точки Ord до точки X - точки пересечения с плоскостью, измеренное в векторах Dir.
Можешь порекомендовать какой нибудь учебник, где будут разъяснены вышеперечисленные понятия, нечто вроде справочника. Для меня даже S = (Dir, n ) представляет загадку 
к сожалению.
к сожалению.Роджерс Д., Алгоритмические основы машинной графики. – М.: Мир, 1989, 512 с.
+ любой учебник по линейной алгебре.
Спасиб!
S - ну, просто некоторая константа.
Dir - направление луча, n - нормаль к плоскости. Если уравнение плоскости Ax+By+Cz+D=0, то координаты нормали = (A,B,C).
Если направление луча перепендикулярно нормали (их скалярное произведение равно нулю то луч параллелен плоскости. Если не параллелен - то точка пересечения считается по приведённой формуле.
Нам требуется пересечь плоскость и луч.
Построим плоскость, содержащую луч и перпендикулярную плоскости (если луч перпендикулярен - возьмём любую плоскость, содержащую луч)
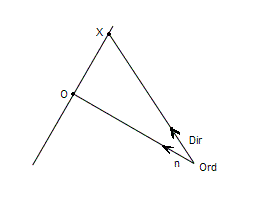
Нам известны: точка Ord (начало луча, точка "наблюдения") направление луча - вектор Dir, уравнение плоскости в виде Ax+By+Cz+D=0.
Надо найти точку пересечения луча с плоскостью - точку X.
"На какую величину S надо умножить Dir , чтобы точка Ord+Dir*S принадлежала плоскости?" (вектор нормали к плоскости N = (A,B,C
X.X=Ord.X+Dir.X*S
X.Y=Ord.Y+Dir.Y*S
X.Z=Ord.Z+Dir.Z*S
подставляем координаты точки X в уравнение плоскости - получаем уравнение вида K*S+Q=0, Q=D+Ord.X*A+Ord.Y*B+Ord.Z*C=D+(Ord,N) - скалярное умножение.
K=Dir.X*A+Dir.Y*B+Dir.Z*C=(Dir,N т.е. S=-Q/K, X=Ord+Dir*S;
X=Ord-(D+(Ord,N/(Dir,N)*Dir;
Dir - направление луча, n - нормаль к плоскости. Если уравнение плоскости Ax+By+Cz+D=0, то координаты нормали = (A,B,C).
Если направление луча перепендикулярно нормали (их скалярное произведение равно нулю то луч параллелен плоскости. Если не параллелен - то точка пересечения считается по приведённой формуле.
Нам требуется пересечь плоскость и луч.
Построим плоскость, содержащую луч и перпендикулярную плоскости (если луч перпендикулярен - возьмём любую плоскость, содержащую луч)
Нам известны: точка Ord (начало луча, точка "наблюдения") направление луча - вектор Dir, уравнение плоскости в виде Ax+By+Cz+D=0.
Надо найти точку пересечения луча с плоскостью - точку X.
"На какую величину S надо умножить Dir , чтобы точка Ord+Dir*S принадлежала плоскости?" (вектор нормали к плоскости N = (A,B,C
X.X=Ord.X+Dir.X*S
X.Y=Ord.Y+Dir.Y*S
X.Z=Ord.Z+Dir.Z*S
подставляем координаты точки X в уравнение плоскости - получаем уравнение вида K*S+Q=0, Q=D+Ord.X*A+Ord.Y*B+Ord.Z*C=D+(Ord,N) - скалярное умножение.
K=Dir.X*A+Dir.Y*B+Dir.Z*C=(Dir,N т.е. S=-Q/K, X=Ord+Dir*S;
X=Ord-(D+(Ord,N/(Dir,N)*Dir;
После того, как мы знаем координаты точки (трёхмерные) внутри плоскости, можем определить её "локальные" координаты в некотором базисе на этой плоскости:
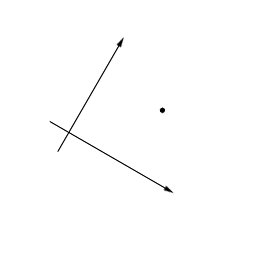
пусть базис задан векторами (u,v) - трёхмерными: u.x,u.y,u.z ну и для v...
вместе с вектором нормали n они должны образовывать базис в трёхмерном пространстве - т.е. быть взаимно ортогональными. (можно ещё и нормировать - но это дело вкуса. имхо ненормированные вектора лучше тем, что если я скажем u "удлиню" или v "укорочу" - то могу управлять масштабом картинки - сжимать/растягивать).
координаты точки "О" - локальное начало координат в плоскости экрана будем считать известной - её координаты также O.x, O.y, O.z
Нам нужно найти коэффициенты (x,y такие что:
X=O+x*u+y*v
X-O=x*u+y*v
умножим скалярно слева и справа на u:
(X-O,u)=x*(u,u)+y*(v,u)=x*|u|, т.к. (v,u)=0
локальная координата x = (X-O,u)/|u| - скалярно вектор u умножается на вектор (X.x-O.x,X.y-O.y,X.z-O.z).
локальная координата y = (X-O,v)/|v| - аналогично.
пусть базис задан векторами (u,v) - трёхмерными: u.x,u.y,u.z ну и для v...
вместе с вектором нормали n они должны образовывать базис в трёхмерном пространстве - т.е. быть взаимно ортогональными. (можно ещё и нормировать - но это дело вкуса. имхо ненормированные вектора лучше тем, что если я скажем u "удлиню" или v "укорочу" - то могу управлять масштабом картинки - сжимать/растягивать).
координаты точки "О" - локальное начало координат в плоскости экрана будем считать известной - её координаты также O.x, O.y, O.z
Нам нужно найти коэффициенты (x,y такие что:
X=O+x*u+y*v
X-O=x*u+y*v
умножим скалярно слева и справа на u:
(X-O,u)=x*(u,u)+y*(v,u)=x*|u|, т.к. (v,u)=0
локальная координата x = (X-O,u)/|u| - скалярно вектор u умножается на вектор (X.x-O.x,X.y-O.y,X.z-O.z).
локальная координата y = (X-O,v)/|v| - аналогично.
Более менее все понятно, но единственный вопрос как определить Dir я не очень понимаю. У нас есть фотография, относительно ее верхнего левого угла мы можем получить некие двумерные координаты животного и кординаты маркеров, которые образуют треугольник. Но на фото мы не можем отметить координаты наблюдателя.
Вот с такой фотографией мне придется иметь дело
При чем такие треугольники покрывают все лежбище.
Применимо ли вышеописанное к этому случаю?
Вот с такой фотографией мне придется иметь дело
При чем такие треугольники покрывают все лежбище.
Применимо ли вышеописанное к этому случаю?
Видимо, у тебя в некотором смысле "обратная" задача. ты бы написал, которые из координат трёхмерные, какие - двумерные - "локальные".
Или больше конкретизируй задачу.
Или больше конкретизируй задачу.
можем ли мы считать, что искажения линейные? хотябы в пределах одного треугольника?
Если нет - то оооочень сложно: нужно знать геометрию линзы (фокусное расстояние, (а если это зум? кол-во элементов в линзе и т.п.)
минимальные "нелинейные" искажения получаются при съёмке с большим фокусным расстоянием и с большей дистанции.
Пример фотографии с большими нелинейными искажениями (оч. короткое фокусное расстояние):
Если нет - то оооочень сложно: нужно знать геометрию линзы (фокусное расстояние, (а если это зум? кол-во элементов в линзе и т.п.)
минимальные "нелинейные" искажения получаются при съёмке с большим фокусным расстоянием и с большей дистанции.
Пример фотографии с большими нелинейными искажениями (оч. короткое фокусное расстояние):
Если задача линейная:
пусть треугольник ABC, точка внутри - P.
мы видим A'B'C', P'
определим величины x,y такие что: A'P'=x*A'B'+y*A'C'
скалярно уможаем на A'B' и на A'C':
x*(A'B',A'B')+y*(A'B',A'C')=(A'P',A'B')
x*(A'B',A'C')+y*(A'C',A'C')=(A'P',A'C')
система линейных уравнений. на x,y.
после того, как x,y найдены - "истинные" координаты точки P определяются:
AP=x*AB+y*AC
повторю, если задача линейная. т.е. треугольники могут быть преобразованы друг к другу сдвигами/поворотами/линейными сжатиями/растяжениями.
пусть треугольник ABC, точка внутри - P.
мы видим A'B'C', P'
определим величины x,y такие что: A'P'=x*A'B'+y*A'C'
скалярно уможаем на A'B' и на A'C':
x*(A'B',A'B')+y*(A'B',A'C')=(A'P',A'B')
x*(A'B',A'C')+y*(A'C',A'C')=(A'P',A'C')
система линейных уравнений. на x,y.
после того, как x,y найдены - "истинные" координаты точки P определяются:
AP=x*AB+y*AC
повторю, если задача линейная. т.е. треугольники могут быть преобразованы друг к другу сдвигами/поворотами/линейными сжатиями/растяжениями.
Я так себе представляю, что я буду иметь дело с двумерными координатами вообще. Т.е. принимается некоторое допущение что маркеры отмечающие треугольники и животные лежащие на лежбище находятся в одной плоскости. Единственно кто имеет некоторую высоту - это наблюдатель фотографирующий животных. Фокусное расстояние объектива составлет около 35 мм, линия горизонта выглядит почти прямой. В этом случае наверное можно считать что преобразования линейны.
Животные на картинках как-то странно выглядят...
В смысле?
У них дневной отдых...
У них дневной отдых...
в приведённых вычислениях нигде не использовалась размерность пространства
Оставить комментарий
grey1970
Помогите найти алгоритм решения данной задачки:A) Имеем на плоскости треугольник с известными координатами вершин. X1Y1 X2Y2 X3Y3
Б) Имеем наблюдателя который смотрит на плоскость под неким неизвестным углом, и видит этот треугольник с некоторомы искажениями. Он определяет координаты треугольника как X1'Y1' X2'Y2' X3'Y3'
В) Имеем некую точку в треугольнике, для которой наблюдатель определмл координаты X'Y'
Необходимо найти координаты точки XY относительно плоскости