Гладко соединить два вектора двумя дугами
Нарисовать пример можешь? А то я не понял, что за касание под 180°.
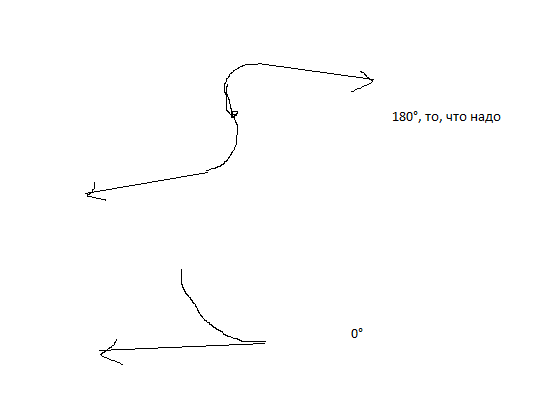
Решений много. Какое нужно-то?
Сделай инверсию в начале одного из векторов, тогда семейство решений строится очень просто. Дальше просто обратную инверсию
Сделай инверсию в начале одного из векторов, тогда семейство решений строится очень просто. Дальше просто обратную инверсию
> Решений много. Какое нужно-то?
Можно ещё потребовать одинаковую кривизну у двух дуг, тогда вроде бы одно решение.
Думал над этой задачей в детстве, ничего особо не придумал кроме как тупо решить квадратное уравнение.
Можно ещё потребовать одинаковую кривизну у двух дуг, тогда вроде бы одно решение.
Думал над этой задачей в детстве, ничего особо не придумал кроме как тупо решить квадратное уравнение.
Спасибо, походу инверсия - то что надо.
А зачем это понадобилось? 

Вектора - касательные к кускам пути фрезы, нужно строить переход с одного куска на другой.
Т.е. дуги обязательно круглые должны быть?
Да. Мне всегда казалось, что некруглая дуга это уже кривая.
Решение есть не всегда. Понятно, что 0 или 180 - это вопрос выбора дуг, нужно просто построить 2 равные окружности, подходящие под условия (такое решение существует и единственно а дуги провести так, как тебе надо. Тут уже либо повезёт, либо нет (картинку влом рисовать).
Поэтому для построения окружностей неважно куда смотрят вектора, важны прямые, на которых они лежат.
Пусть A начало первого вектора, B - второго, C - точка пересечения этих 2х прямых (условие, что дуги построятся, эквивалентно условию, что один из векторов смотрит на C, другой нет). Пока дальше идей нет, правда только квадратное уравнение на радиус окружности, типа
координаты одного центра - A + ra (a ортогонально AC, плюс надо направление правильно задачть другого - B + rb, уравнение
|(A - B) + r(a - b)|^2 = 4r^2.
С инверсией можно было построить красиво, но там равенство окружностей паршиво следить.
Поэтому для построения окружностей неважно куда смотрят вектора, важны прямые, на которых они лежат.
Пусть A начало первого вектора, B - второго, C - точка пересечения этих 2х прямых (условие, что дуги построятся, эквивалентно условию, что один из векторов смотрит на C, другой нет). Пока дальше идей нет, правда только квадратное уравнение на радиус окружности, типа
координаты одного центра - A + ra (a ортогонально AC, плюс надо направление правильно задачть другого - B + rb, уравнение
|(A - B) + r(a - b)|^2 = 4r^2.
С инверсией можно было построить красиво, но там равенство окружностей паршиво следить.
залезать в расчеты не хочетсякак же без этого?

Да. Мне всегда казалось, что некруглая дуга это уже кривая.Неломаная кривая не обязана быть частью окружности.
Просто если не важен вид кривой, то могут быть более простые решения.
Как вариант: Кривая Безье.
станок с чпу делаешь?
Решение есть не всегда.Спасибо еще раз за идею с инверсией, несколько часов проебавшись с направлениями написал функцию. Решения, похоже, нет только на множестве меры 0. Правда теперь остается проблема избежать решений типа такого (самое здоровое):

Сиреневое - векторы, белое - дуги.
станок с чпу делаешь?Пишу код, который генерирует код для станка с чпу.
Имелось ввиду для условия равной кривизны, решение есть не всегда. А именно в половине случаев.
Имелось ввиду для условия равной кривизны, решение есть не всегда. А именно в половине случаев.Что-то ты гонишь, по-моему.
Вектора - касательные к кускам пути фрезы, нужно строить переход с одного куска на другой.я подозреваю что могут возникнуть проблемы в местах перехода с одной дуги на другую и с вектора на дугу - разрав кривизны имеется
подозреваю, что возможно повреждение фрезы/материала
Собственно если фреза - плоский диск, то 99% возникнут проблемы
В САПР типа Catia для таких операций используются сплайны - кривые с сохранением кривизны. Там кстати можно чертежи чертить. Может тебе и подойдет. Правда это как из пушки по воробьям =)
Сплайн для соединения двух векторо нужен будет только один - а не две дуги как у тебя. Как он задается математически не знаю. Вообще за использование двух дуг вместо сплайна в хорошем инженерном вузе двойку ставят =)
И разумеется уже никто не пишет вручную код для ЧПУ. Обработка моделируется в Catia, а потом выгружается в станок. Программировать вообще не надо - это технологии 80х
разрав кривизны имеетсяподозреваю, что возможно повреждение фрезы/материалаНет. Например все станки поддерживают отрезки и дуги, ежу понятно что отрезок+дуга=скачок кривизны. 1-раз дифференцируемости вполне достаточно.
Сплайн для соединения двух векторо нужен будет только один
А вот сплайны поддерживают далеко не все. Можно, конечно, построить сплайн и аппроксимировать ломанной, но тогда получится много маленьких отрезков, что плохо.
Обработка моделируется в Catia, а потом выгружается в станок.
Собственно эту Catia я и пишу. Только не Catia.
А почему тогда именно две дуги? 

ну ок, тебе видней =) Я больше вопросами 3Д моделлинга занимался. Там за прямая+дуга убивать надо. Если это, конечно, не кондовый машиностроительный объект
Да, действительно. А значит, и решение не единственно. Перебирать придётся.
А почему тогда именно две дуги?Можно, наверное, и три дуги
 Но хотелось решить задачу с двумя.
Но хотелось решить задачу с двумя.Можно, наверное, и три дугиЯ на самом деле хотел сказать, что в некоторых случаях вместо больших дуг гораздо "красивее" получится 2 дуги + отрезок. А ещё многое можно одной дугой соединить (хотя это формально можно под 2 подогнать).Но хотелось решить задачу с двумя.
Да, похоже есть случаи, когда решение с двумя дугами неприемлимо, как его ни оптимизируй.
посмотри на википедии статью про B-сплайны (basic splines) на русском и английском (ссылку не могу дать, тк в фдс пока нет инета ). Там была анимация, демонстрирующая как строится B-сплайн
Оставить комментарий
Devid
Есть два вектора на плоскости, нужно провести две дуги окружностей так, чтобы первая дуга касалась первого вектора, вторая второго и чтобы дуги касались друг друга. Все касания под углом 180 (не 0).Может, есть стандартное решение, а то залезать в расчеты не хочется?