Программа пересчёта из одной системы координат в другую
man аффинные преобразования, что ли?
Вообщем то, насколько я понимаю, тебе надо только матрицу 2х2 для двумерного случая или 3х3 для трехмерного (ты сам то определись, а то по картинкам не ясно) задать, а потом соответсвие будеи искаться как матрицца * исходный вектор.
При чем тут программирование?
Лучше бы с Study написал.
Вообщем то, насколько я понимаю, тебе надо только матрицу 2х2 для двумерного случая или 3х3 для трехмерного (ты сам то определись, а то по картинкам не ясно) задать, а потом соответсвие будеи искаться как матрицца * исходный вектор.
При чем тут программирование?
Лучше бы с Study написал.
Интересует пока только двумерный случай. А в программировании, потому что программа будет пересчитывать. :-) Хотя, наверное, в Стади бы лучше было, но как-то привык здесь спрашивать.
В стади тя задвинут сразу, у тя жвторая тоже плоская и раскладываешь линейно по векторам -т.е. у тебя во второй системе координаты не однозначно задаются. Собственно вторая система координат поэтому как-то не конструктивна что ли.
А так задай базовые вектора прямоугольной какой-нить комбинацией векторов во второй, получишь некий вариант "координат"
А так задай базовые вектора прямоугольной какой-нить комбинацией векторов во второй, получишь некий вариант "координат"
Плохо понимаю. Как это сделать на конкретном примере с теми же точками a и b (см. верхний рис.). С какими координатами они получатся на нижней системе координат?
На нижней системе координаты точек определены неоднозначно. Т.е. например (1, 1, 1) и (0, 0, 0) задают одну и ту же точку.
Например,
любая точка (x,y) будут иметь координаты (2*x/sqrt(30,y+x/sqrt(3 или (2*x/sqrt(3)+k,k,y+x/sqrt(3)+k) k любое и куча других вариантов
любая точка (x,y) будут иметь координаты (2*x/sqrt(30,y+x/sqrt(3 или (2*x/sqrt(3)+k,k,y+x/sqrt(3)+k) k любое и куча других вариантов
пиздец
кстати а нах на втором рисунке третья ось?
там третья ось как третья нога просто.
аффтару - заботай несколько страниц обычного учебника по ангему.
аффтару - заботай несколько страниц обычного учебника по ангему.
Во-первых, зафиксируй центр второй системы всё-таки. Иначе ничего не получится.
Во-вторых, всё довольно просто: если у тебя есть базисные вектора e1 и e2, то координатами точки x в этом базисе называются числа a и b такие, что x = a*e1 + b*e2. Для трёхмерного случая аналогично. Теперь берёшь, расписываешь системку линейных уравнений и решаешь аналитически (то бишь находишь какой-нибудь мапл и заставляешь его обратить матрицу. Или сам обращаешь по формуле кого-то там).
Если я правильно помню, можно эту обращённую матрицу как-то просто выразить через скалярные произведения искомого вектора на инверсные базисные (как в случае ортогонального базиса подпатченные при помощи скалярных произведений между базисными векторами.
Во-вторых, всё довольно просто: если у тебя есть базисные вектора e1 и e2, то координатами точки x в этом базисе называются числа a и b такие, что x = a*e1 + b*e2. Для трёхмерного случая аналогично. Теперь берёшь, расписываешь системку линейных уравнений и решаешь аналитически (то бишь находишь какой-нибудь мапл и заставляешь его обратить матрицу. Или сам обращаешь по формуле кого-то там).
Если я правильно помню, можно эту обращённую матрицу как-то просто выразить через скалярные произведения искомого вектора на инверсные базисные (как в случае ортогонального базиса подпатченные при помощи скалярных произведений между базисными векторами.
А можно проще и на примере. Объясню зачем мне три оси. У меня будут три датчика, которые будут установлены на равном расстоянии друг от друга по углам равностороннего треугольника. На эти датчики будет опираться плоская платформа, передающая нагрузку на датчики. Проблема состоит в том, что данные от трех датчиков нужно пересчитать в координаты точки перемещения нагрузки.
Например, при одинаковой нагрузке на датчики точка будет в начале системы координат.
Если бы датчиков было четыре, которые распложены крестом, было бы понятно. Как в моём случае пересчитать?
Например, при одинаковой нагрузке на датчики точка будет в начале системы координат.
Если бы датчиков было четыре, которые распложены крестом, было бы понятно. Как в моём случае пересчитать?
это же надо найти координаты центра масс.
как быстро постановка задачи меняется...
как быстро постановка задачи меняется...

от задачи 1-го курса перешли к школьной задаче
СзМ
СзМ
слушай
ну правда, открой же уже школьный учебник по математике
дело в том что мы все с тобой разговариваем на разных языках
ось координат - это конкретное определение в математике
координаты точки - конкретное определение в математике
ты же под осью понимаешь показание датчиков
в твоем понимании может это и нормально, но в математическом - это бред
ну правда, открой же уже школьный учебник по математике
дело в том что мы все с тобой разговариваем на разных языках
ось координат - это конкретное определение в математике
координаты точки - конкретное определение в математике
ты же под осью понимаешь показание датчиков
в твоем понимании может это и нормально, но в математическом - это бред
это совершенно не бред — напротив, это вполне корректное определение системы координат. Однако надо было сразу объяснить, что понимается под координатами.
Задача сводится к решению уравнения
F1*r1 + F2*r2 + F3*r3 = 0
при условии, что
r1 = a + r2 = b + r3
где a, b, r — векторы (а и b — сторон, r - от углов до искомой точки F — скалярные показания датчиков.
Ответ:
r1 = (F2*a + F3*b)/(F1+F2+F3)
Если масса известна, достаточно двух датчиков и фиксированного закрепления.
Все это верно для горизонтальной невесомой твердой платформы.
Надеюсь, не напутал.
Задача сводится к решению уравнения
F1*r1 + F2*r2 + F3*r3 = 0
при условии, что
r1 = a + r2 = b + r3
где a, b, r — векторы (а и b — сторон, r - от углов до искомой точки F — скалярные показания датчиков.
Ответ:
r1 = (F2*a + F3*b)/(F1+F2+F3)
Если масса известна, достаточно двух датчиков и фиксированного закрепления.
Все это верно для горизонтальной невесомой твердой платформы.
Надеюсь, не напутал.
r1 = (F2*a + F3*b)/(F1+F2+F3)пипец ты уравнения расписал
а в итогде написал определение центра масс
токо-ты еще и третью слагаемую умудрился потерять
http://ru.wikipedia.org/wiki/%D0%A6%D0%B5%D0%BD%D1%82%D1%80_...
да, действительно, центр масс, я ступил.
Нет, не потерял третьей слагаемой, третья-то координата равна нулю.
Нет, не потерял третьей слагаемой, третья-то координата равна нулю.
Это все замечательно, только как пересчитывать я так и не понял. Есть три точки, на которой находится платформа. Надо перейти от скалярных величин, измеренных с каждого из трех датчиков к координатам точки центра масс. Результирующая система координат должна быть обычная прямоугольная. Не знаю, мне кажется что начальная постановка задачи близка по сути с тем, что надо получить. или я не прав? Не помню я что-то в школьных учебниках подобных задач.
Ответ:Про F1,F2,F3 я понял, а что даст r1, a и b? Мне же в результате надо два числа: 1. координату X и координату Y центра масс.
r1 = (F2*a + F3*b)/(F1+F2+F3)
Это простая в принципе, но сложная в реализации задача, известная как Vector Components Problem. Опытные люди с ней справятся за пару часов. Готов запрограммировать ее за 1000 рублей и пачку сока на нужном тебе языке.
deleted
Я за 900 наваяю библиотеку =)
Я за тридцатку порекомендую учебник геометрии для десятого класса. 

не обламывай бизнес
Это простая в принципе, но сложная в реализации задача, известная как Vector Components Problem. Опытные люди с ней справятся за пару часов. Готов запрограммировать ее за 1000 рублей и пачку сока на нужном тебе языке.Отлично. Давай применим искусственные нейросети.

To All:
Правильно ли я понял, что координаты интересующей точки можно найти по следующей формуле, подставляя координаты каждой из трех точек датчиков (xk, yk, zk) и мгновенные значения веса, измереннные от тех же точек (mk при каждой координате). М - масса всей системы?
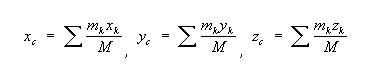
Оставить комментарий
dimon72
Нужно решить такую задачу (неважно на чём, можно на Delphi). Есть некая система координат XOY. Требуется найти соответствие точек из этой системы координат в другой системе координат Х1Х2Х3, у которой оси расположены под углом 120 град. Для примера возьмем точку а(2;2) и переместим её в b(2;3) (в прямоугольной системе). Как будет выглядеть аналогичная операция а->b в нижней системе координат? Какие будут значения по координатам?Чувствую, что какая-то простая линейная формула должна быть, но не могу догнать какая. В Инете ответа не нашёл. Может кто знает как пересчитывать точки из одной системы в другую?