удивительная дейкстра для разреженных графов без куч. [омг]
непон, в стэке вершина вместе с расстоянием до нее лежит? И если несколько раз попадает, то... Не совсем понял.
в стеке лежит вершина. с которой непосредственно связан ее вес - текущее найденное расстояние до нее от исходной
А граф как задан?
Если матрицей связности, то поиск смежных вершин для каждой вершины - это O(N).
Добавление в упорядоченный стек - тоже O(N а в кучу O(logN). Но это суммируется с O(N).
Отсюда получается, что любая структура для хранения очереди на обработку будет работать одинаково быстро, если добавление и удаление не медленнее O(N).
Правда, пока что я не уверен в этом вашем стеке:
Если матрицей связности, то поиск смежных вершин для каждой вершины - это O(N).
Добавление в упорядоченный стек - тоже O(N а в кучу O(logN). Но это суммируется с O(N).
Отсюда получается, что любая структура для хранения очереди на обработку будет работать одинаково быстро, если добавление и удаление не медленнее O(N).
Правда, пока что я не уверен в этом вашем стеке:
в стек одна и та же вершина может добавляться более одного раза. но не смотря на это стека размера V хватает и он не переполняется.Мне кажется, можно придумать хитрый контр-пример, когда размера стека не хватит.
пример графа.
это граф путей для ТЦ
1, 2 этаж, плюс парковка на хуеву тучу мест. ноды расставлены по коридорам и магазинам так, чтобы более менее ништяк пути получались.
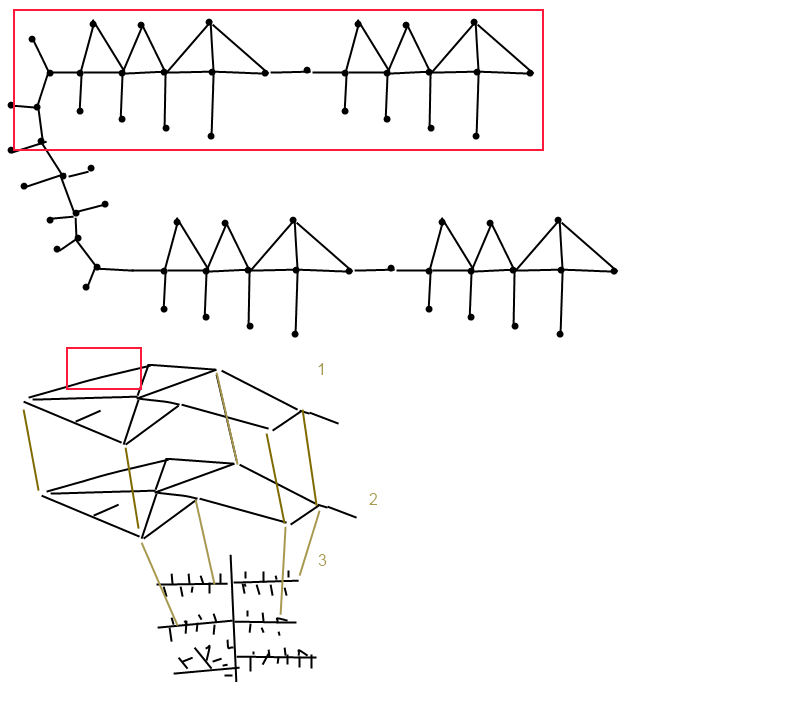
это граф путей для ТЦ
1, 2 этаж, плюс парковка на хуеву тучу мест. ноды расставлены по коридорам и магазинам так, чтобы более менее ништяк пути получались.

граф задан конечно же списками связности
Мне кажется, можно придумать хитрый контр-пример, когда размера стека не хватит.это да. но для нашего графа (см рисунок) все работает.
Добавление в упорядоченный стек - тоже O(N а в кучу O(logN). Но это суммируется с O(N).Там про граф что-то дополнительно известно, позволяющее добавлять и свапать в константное время.
А какая сложность добавления и удаления твоей ОСП на базе массива была? Мне кажется, что вариант коллеги асимптотически медленнее, но граф слишком мал, чтобы это сказалось.
ну stupid-реализация очереди с приоритетами на базе массива такая:
сначала вес всех вершин ставим бесконечность. и складываем их подряд в массив.
decrese-key работает константу. просто берем и меняем значение элемента в массиве.
извлечение минимальной всегда стабильно ровно за V шагов. - просматриваем весь массив и находим минимум из еще не обработанных вершин
итого V*V+E
сначала вес всех вершин ставим бесконечность. и складываем их подряд в массив.
decrese-key работает константу. просто берем и меняем значение элемента в массиве.
извлечение минимальной всегда стабильно ровно за V шагов. - просматриваем весь массив и находим минимум из еще не обработанных вершин
итого V*V+E
Ну смотри, пусть N вершин, и из каждой выходит не более V ребер.
Тогда сложность реализации Дейсктры:
N вершин * (T1 время поиска и удаления лучшей вершины из очереди с приоритетом) * (обработка каждой из V смежных вершин) * (T2 время добавления в ОСП новой вершины).
Т.е. O(N*V*T1*T2)
В случае кучи T1 = T2 = O(logN и сложность O(N * V * (logN)^2)
В случае коллеги T1 = O(1 T2 = O(N общая сложность O(N^2 * V).
У него медленнее, но для 2400 вершин это пофигу.
Заметь, T2=O(N) только в том случае, если мы ВЕРИМ в то, что весь стек уместится в N. А в общем случае там O(N*V а общая сложность O(N^2 * V^2).
Тогда сложность реализации Дейсктры:
N вершин * (T1 время поиска и удаления лучшей вершины из очереди с приоритетом) * (обработка каждой из V смежных вершин) * (T2 время добавления в ОСП новой вершины).
Т.е. O(N*V*T1*T2)
В случае кучи T1 = T2 = O(logN и сложность O(N * V * (logN)^2)
В случае коллеги T1 = O(1 T2 = O(N общая сложность O(N^2 * V).
У него медленнее, но для 2400 вершин это пофигу.
Заметь, T2=O(N) только в том случае, если мы ВЕРИМ в то, что весь стек уместится в N. А в общем случае там O(N*V а общая сложность O(N^2 * V^2).
Ну смотри, пусть N вершин, и из каждой выходит не более V ребер.это очень грубая оценка, надо считать V вершин и E ребер в сумме.
N вершин * (T1 время поиска и удаления лучшей вершины из очереди с приоритетом) * (обработка каждой из V смежных вершин) * (T2 время добавления в ОСП новой вершины).неправильно второе умножение. должен быть плюс
N * (find + смежные * push)
давай стандартные обозначения
вершин V
всех ребер E
ступид реализация дает:
V*(V) + E*1 = V*2
для кучи
V * (logV) + E * LogV = E logV
Реализация с тупой очередью:
T1 = O(N T2 = O(1 общая сложность O(N^2 * V как и у коллеги.
У него, конечно, константа при этой асимптотике значительно меньше, т.к. ты на каждом шаге поиска минимума пробегаешь РОВНО N вершин, а он при вставке - не больше, чем размер стека. Плюс граф хороший (я так понял, что из планарных кусков так что вставка работает значительно быстрее своей асимптотики.
T1 = O(N T2 = O(1 общая сложность O(N^2 * V как и у коллеги.
У него, конечно, константа при этой асимптотике значительно меньше, т.к. ты на каждом шаге поиска минимума пробегаешь РОВНО N вершин, а он при вставке - не больше, чем размер стека. Плюс граф хороший (я так понял, что из планарных кусков так что вставка работает значительно быстрее своей асимптотики.
Тьфу, точно, думал же я, что будет плюс.
Тогда:
Твоя тупая версия: N*(N + V*1) = N^2 + NV
Твоя хорошая версия: N*(logN + V*logN) = NV*logN
Коллега: N*(1 + V*N) = N^2*V
Все решает константа при втором слагаемом. Реально там не N, а скорее порядка V величина.
Тогда:
Твоя тупая версия: N*(N + V*1) = N^2 + NV
Твоя хорошая версия: N*(logN + V*logN) = NV*logN
Коллега: N*(1 + V*N) = N^2*V
Все решает константа при втором слагаемом. Реально там не N, а скорее порядка V величина.
P.S. Короче, ты решил задачу хорошо для любого разреженного графа, а коллега еще использовал то, что граф "евклидов" (вес ребра равен длине для определенного представления в R3) и красив.
Твоя тупая версия: N*(N + V*logN) = N^2 + NV*logNтупая в твоих обозначениях так: N*(N + V*1) = N^2 + NV
Коллега: N*(1 + V*N) = N^2*Vправильно. вот я и просил ее оценить в первом посте этой темы
Все решает константа при втором слагаемом. Реально там не N, а скорее порядка V величина.
да, в тупой версии протупил. Исправляю 

Еще раз, эти оценки очень грубые и нормально работают как раз только когда твое V довольно мало (3-4, не больше  )
)
Известная теоретическая оценка для дейкстры по времени — ElogV + VlogV, где E — общее число ребер, V — число вершин. Для очереди на массиве — V^2 + E. Есть еще фибоначчиевы кучи, где получается E + VlogV, но там как раз большая константа и слишком много указателей, говорят, медленнее они работают зачастую.
 )
)Известная теоретическая оценка для дейкстры по времени — ElogV + VlogV, где E — общее число ребер, V — число вершин. Для очереди на массиве — V^2 + E. Есть еще фибоначчиевы кучи, где получается E + VlogV, но там как раз большая константа и слишком много указателей, говорят, медленнее они работают зачастую.
ну да, я знаю, что оценки грубые. Но тут-то как раз кол-во ребер, инцидентных вершине, очень мало, вот я и позволил себе такую вольность.
А сложность Дейкстры вообще - такого не бывает. Бывает сложность Дейкстры при данном представлении графа и при данной структуре очереди вершин.
А сложность Дейкстры вообще - такого не бывает. Бывает сложность Дейкстры при данном представлении графа и при данной структуре очереди вершин.
да нет. нормальные оценки. можно считать, что граф довольно равномерный (а так в принципе и есть и с каждой выходит равное количество ребер.
почему они грубые. если они даже точные (для равномерного графа). в его терминах
почему они грубые. если они даже точные (для равномерного графа). в его терминах
Коллега: N*(1 + V*N) = N^2*V
Все решает константа при втором слагаемом. Реально там не N, а скорее порядка V величина.
то, что граф "евклидовто что граф евклидов можно использовать и допилить реализацию соседа так, чтобы она работала не хуже N*N даже для полного графа, а не за N^3)
просто не будем добавлять вершины по несколько раз в стек. заведя спец метку для этого.
> в стек кладем за линейное время. сначала наверх, а потом опускаем вниз, все время свапая, сохраняя упорядоченность в стеке.
Ты уверен, что не в конец? Тогда при более менее равномерной длине ребра свапов вообще почти не будет происходить.
А еще в стеке хранится только фронт, для плоских графов он V^{1/2}, а не V (может, у вас специфическая ситуация, замерь размер стека).
Если размер стека порядка 10, то ты хоть пузырьком сортируй.
Ты уверен, что не в конец? Тогда при более менее равномерной длине ребра свапов вообще почти не будет происходить.
А еще в стеке хранится только фронт, для плоских графов он V^{1/2}, а не V (может, у вас специфическая ситуация, замерь размер стека).
Если размер стека порядка 10, то ты хоть пузырьком сортируй.
как ты себе представляешь пихание вершины в конец стека?
на счет фронта да. очень похоже на то, но там вершины по несколько раз попадаются ведь
на счет фронта да. очень похоже на то, но там вершины по несколько раз попадаются ведь
дэк. Он ведь тоже стэк.
Ну, я просто уточнить, а вдруг.
Ну, я просто уточнить, а вдруг.
Если у тебя дерево, то только 1 раз. Если длины рёбер равномерны, то почти не будет повторений. Повторения бывают, когда в одну вершину ведут два или более почти одинаковых пути, таких почти во всех разреженных графах (а тем более на реальных метриках) единицы. То есть на общую скорость это ваще не влияет
Короче, можно считать, что для такого графа дейкстра вырождается почти в алгоритм волны, где вместо очереди с приоритетом вершины засовываются в обычную очередь, и время добавления и удаления (T1 и T2 в моих обозначениях) сравнимы с 1.
оке. согласен со всем, что написал _SS_.
просто повезло, что фронт очень маленький.и в конец в самом деле было бы лучше добавлять. А еще лучше перевернуть стек. брать из начала массива, сдвигая указатель, а добавлять в конец массива
просто повезло, что фронт очень маленький.и в конец в самом деле было бы лучше добавлять. А еще лучше перевернуть стек. брать из начала массива, сдвигая указатель, а добавлять в конец массива
А еще лучше перевернуть стек. брать из начала массива, сдвигая указатель, а добавлять в конец массиваочередь называется

проблема в том, что у нас еще есть кое-какие специальные ребра. скажем ребра перехода с этажа на этаж имеют довольно большой вес.
плюс еще есть лифты. скажем есть ребра
1этаж-2этаж = 1000
2этаж-3этаж = 1000
плюс читы вида 1этаж-3этаж=1999
плюс есть угловые магазины у которых два входа. а нам не нужно чтобы путь из А в Б срезался через такие углы, поэтому эти ребра мы чуток поднимаем по весу
плюс еще есть лифты. скажем есть ребра
1этаж-2этаж = 1000
2этаж-3этаж = 1000
плюс читы вида 1этаж-3этаж=1999
плюс есть угловые магазины у которых два входа. а нам не нужно чтобы путь из А в Б срезался через такие углы, поэтому эти ребра мы чуток поднимаем по весу
ну да, я же сказал, "почти" в алгоритм волны. Т.е. какие-то перестановки в этой очереди делать все равно придется. Но так как их мало, то можно их делать пузырьком, как твой коллега.
Кстати, я сразу так и думал, что у коллеги не стек, а очередь - добавляет с одной стороны, а удаляет с другой.
Кстати, я сразу так и думал, что у коллеги не стек, а очередь - добавляет с одной стороны, а удаляет с другой.
да. конечно обычная же очередь. просто в ней не все элементы. а только фронт.
плюс такой реализации еще в том, что она меньше памяти жрет по сравнению с кучами
ибо не нужно хранить ссылки на позиции элементов в куче
плюс такой реализации еще в том, что она меньше памяти жрет по сравнению с кучами
ибо не нужно хранить ссылки на позиции элементов в куче
так в куче же тоже только фронт можно хранить, разве нет?
кстати да! 
но не буду дописывать. и так уже мгновенно работает

но не буду дописывать. и так уже мгновенно работает
Оставить комментарий
lubanj
Есть у нас на работе довольно разреженный граф.Вершин 2400. Из каждой обычно лишь 5..максимум 10 ребер. граф задан списками связности
Реализация с очередью с приоритетами на базе массива работает как и положено довольно долго (1-2сек на мобиле).
Переписал сегодня при помощи кучи. Работает мгновенно, как и должно. НО! обнаружил у соседа забавную реализацию. без куч. работает тоже мгновенно. и корректно. она эквивалента алгоритму дейкстры.
имеем стэк, который будет играть роль очереди с приоритетами. он постоянно в отсортированном состоянии. наверху - минимальный элемент.
в начале в нем стартовая вершина.
все вершины белые
пока (не покрасили в черный все вершины) {
извлекаем вершину
обрабатываем все смежные с нею {
если она черная, то continue;
если изменяем расстояние до вершины, то кладем ее в стэк.
}
красим вершину в черный цвет.
}
в стек кладем за линейное время. сначала наверх, а потом опускаем вниз, все время свапая, сохраняя упорядоченность в стеке.
в стек одна и та же вершина может добавляться более одного раза. но не смотря на это стека размера V хватает и он не переполняется.
очевидно, что на каждом шаге мы действительно извлекаем самую минимальную вершину из нашей очереди. В которой просто не лежат вершины с бесконечным весом. А все, у которых мы вес изменяем, попадают в очередь.
мне обидно стало, что такая реализация работает так быстро. кто-нибудь может оценить время работы?