Сколько надо параметров для задания эллипса? [Re: Как нарисовать эллип
А какие еще нужнжы? 
не 4х должно хватить.
наверное имуются ввиду ещё и направления полуосей?
центр.
длины осей.
и поворот.
итого 5.
автор трэда наверно имеет в виду что одна ось вертикальна.
длины осей.
и поворот.
итого 5.
автор трэда наверно имеет в виду что одна ось вертикальна.
Даже если одна ось вертикальна, то можно построить как минимум два разных эллипса с одинаковыми другими четырьмя параметрами 
Они совпадут? 
Костик, не расстраивай меня. Один из другог о получится поворотом на 90 градусов.
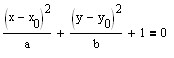
И как жэ?
Оси переподписывать не по-джентельменски
Вообще-то 4-х параметров многовато.
Достаточно трех.
Достаточно трех.
прикольная у тебя формула 
для мнимого эллипса, видать.
во-первых, в знаменателях a^2, b^2
во-вторых не ....+1=0, а ....=1
для мнимого эллипса, видать.во-первых, в знаменателях a^2, b^2
во-вторых не ....+1=0, а ....=1
a vot i ne sovsem naprimer, dlya
a = -c²
b = -d²
poluchaetsya obychnyi ellips
naprimer, dlyaa = -c²
b = -d²
poluchaetsya obychnyi ellips
2 давай сюда на паскале!
Фигню написал. Двух полуосей и координат центра недостаточно. Ты в своей формуле предполагаешь порядок этих осей - то есть что а по иксу, а б по игреку. А это не есть правильно. Если известно, что оси веритикальные, известны координаты центра и размеры полуосей, то можно по этим параметрам написать две разные формулы и будет два разных эллипса.
Ага, а ещё можно предположить, что "а" - это х координата центра, "х" - это длина оси по у, и т.д.
Итого 4! = 24 варианта на самом деле.
Сатурн, не неси фигню =)
Итого 4! = 24 варианта на самом деле.
Сатурн, не неси фигню =)
Блин, на , похоже, остался 
в январе смогу библиотеку дать (там tpu-шная самописная библиотека, заменяющая модуль Graph для 256-битного рисования. Содержит почти все те же функции, что и Граф, не умеет делать заливку текстурой, зато умеет делать заливку до разноцветного контура)
вот ссылка на чью-то чужую на Си:
http://mike.nov.ru/rus/read/graphics/Ellipse-C/
в январе смогу библиотеку дать (там tpu-шная самописная библиотека, заменяющая модуль Graph для 256-битного рисования. Содержит почти все те же функции, что и Граф, не умеет делать заливку текстурой, зато умеет делать заливку до разноцветного контура)вот ссылка на чью-то чужую на Си:
http://mike.nov.ru/rus/read/graphics/Ellipse-C/
ФЖ, сам не неси фигню. Лучше подумай над моим первым постом.
Предлагаю остановиться на следующем:
Для произвольного эллипса - необходимо 5 параметров, для ориентированого вдоль осей x&y, при соответствующей договоренности, достаточно 4 параметра.
Для произвольного эллипса - необходимо 5 параметров, для ориентированого вдоль осей x&y, при соответствующей договоренности, достаточно 4 параметра.
А чего тут думать?
Если мы рисуем эллипс с осями, параллельными осям координат, то четыре параметра его задают однозначно. Спекуляции на тему "а с чего вы взяли, что третий параметр - это его ширина именно по оси х, а не по оси у" - это не более чем спекуляции, что я и показал, логически их завершив, продемонстрировав 24 варианта.
Если мы рисуем эллипс с осями, параллельными осям координат, то четыре параметра его задают однозначно. Спекуляции на тему "а с чего вы взяли, что третий параметр - это его ширина именно по оси х, а не по оси у" - это не более чем спекуляции, что я и показал, логически их завершив, продемонстрировав 24 варианта.
С даркгреем полностью согласен, а ты несёшь чушь. Если ты повернёшь свой эллипс на 90 градусов, то получишь новый эллипс с теми же самыми четырьмя параметрами, и оси у него будут параллельны осям координат. Но это будет другой эллипс. И никаких спекуляций.
Если я поверну эллипс, задаваемый упорядоченной четверкой чисел (0, 0, 2, 3) на девяносто градусов, я получу эллипс, задаваемый упорядоченной четвёркой чисел (0, 0, 3, 2). Это разные эллипсы и разные четвёрки чисел.
Вопрос на засыпку: а если ты его повернёшь на 45 градусов, то как твоя четвёрка чисел будет упорядочена?
Ну естесвенно смысл упорядочивания есть только когда оси совпадают с координатными. Но это ведь именно этот случай.
Все.
Это полный пипец!
Я поддерживаю FJ.
Википедия
Што за флуд развели?
Итак, невырожденный эллипс задается пятеркой чисел.
Эта пятерка чисел упорядочена, естественно.
Это полный пипец!
Я поддерживаю FJ.
Википедия
Што за флуд развели?
Итак, невырожденный эллипс задается пятеркой чисел.
Эта пятерка чисел упорядочена, естественно.
Если эллипс повернётся на 45 градусов, то его оси не будут параллельны осям координат, и задать его при помощи четвёрки чисел, предназначенной для задания эллипсов, чьи оси параллельны осям координат, будет невозможно.
Как ты не понимаешь таких простых вещей?
Как ты не понимаешь таких простых вещей?
Итак, невырожденный эллипс задается пятеркой чисел.Костик, всё правильно. Я асболютно согласен с тобой.
Эта пятерка чисел упорядочена, естественно.
Я это и утверждаю. Что она упорядочена. А ФЖ пытается мне доказать, что при повороте эллипса на 90 градусов третий и четвёрный параметры меняются местами. Смешно, не правда ли?
С чего начался спор? С того, что было высказано утверждение, что если задать четыре параметра эллипса, и сказать, что его оси параллельны осям координат, то эллипс будет задан однозначно. Это утверждение неверно. Вот погляди на два эллипса (поворот в градусах):
(0, 0, 5, 6, 0) и (0, 0, 5, 6, 90)
Четыре параметра у этих эллипсов совпадают. Оси обоих эллипсов параллельны осям координат. И эллипсы НЕ совпадают.
Ещё вопросы будут?
Чем отличается эллипс (0, 0, 6, 5, 0) от эллипса (0, 0, 5, 6, 90)?
Первые два параметра задают центр эллипса.
Ты рассматриваешь эллипсы не как геометрические места точек? А как?
Первые два параметра задают центр эллипса.
Ты рассматриваешь эллипсы не как геометрические места точек? А как?
> (0, 0, 6, 5, 0) от эллипса (0, 0, 5, 6, 90)
он несколько иное написал
он несколько иное написал
Я знаю, он сам себе противоречит.
Сперва он посмеялся, что 3-й и 4-й параметры меняются местами, а потом в опровержение этого привел пример, где местами их не поменял.
Сперва он посмеялся, что 3-й и 4-й параметры меняются местами, а потом в опровержение этого привел пример, где местами их не поменял.
Правильно, валеночек мой!
Эти два эллипса совпадают. А ещё с ними совпадает, например, (0, 0, 6, 5, 180). Но у приведённых тобой эллипсов разные полуоси.
Эти два эллипса совпадают. А ещё с ними совпадает, например, (0, 0, 6, 5, 180). Но у приведённых тобой эллипсов разные полуоси.
Мэдди, включи мозг и подумай. Я себе не противоречу.
Да, я поменял 3-й и 4-й параметр местами.
Почему этого не сделал ты, мой пирожок?
Почему этого не сделал ты, мой пирожок?
А с какой радости я их должен менять? Пятёрка упорядоченная.
Не осилил слов. Сатурн, чтобы донести до благодарного читателя смысл твоих слов, напиши, пожалуйста, функцию, которая будет рисовать эллипс по-твоему (можешь забить на целочисленную арифметику, ибо не в ней дело). В конце концов, алгоритм это наиболее однозначная форма объяснения.
Так.
Приведи пример, опровергающий следующую гипотезу:
Эллипс, оси которого параллельны осям координат, однозначно определяется упорядоченной четверкой (x, y, w, h где (x, y) - центр эллипса, w - длина горизонтальной оси эллипса, h - вертикальной (w > 0, h > 0).
Тебе нужно привести пример двух несовпадающих эллипсов, для которых соответствующие упорядоченные четверки будут одинаковые.
Везде под эллипсом я понимаю множество точек, которое он задает.
Приведи пример, опровергающий следующую гипотезу:
Эллипс, оси которого параллельны осям координат, однозначно определяется упорядоченной четверкой (x, y, w, h где (x, y) - центр эллипса, w - длина горизонтальной оси эллипса, h - вертикальной (w > 0, h > 0).
Тебе нужно привести пример двух несовпадающих эллипсов, для которых соответствующие упорядоченные четверки будут одинаковые.
Везде под эллипсом я понимаю множество точек, которое он задает.
В общем, для тех, кто не понял: я к фразе придрался. Если бы там было сказано: пятый параметр (то бишь поворот) равен нулю, то я бы и не пикнул, ибо тогда действительно всё было бы однозначно. Но там было сказано: оси параллельны осям координат. Что сразу порождает два непересекающихся класса эллипсов, подходящих под это утверждение - с углом поворота pi * n и с углом pi * n + pi / 2.
Ты рассматриваешь эллипсы не как множества точек?
Я уже привёл в качетве примера два эллипса, у которых эта упорядоченная четвёрка совпадает, а различаются только углы поворота. И эти эллипсы не совпадают, как множества!
С чего ты взял?
Нет.
Ты привел примеры, у которых упорядоченная 5-ка совпадает.
А теперь забудь про неё, прочитай, что из себя представляет моя упорядоченная четверка и построй её для этих эллипсов.
Ты получишь (0, 0, 5, 6) и (0, 0, 6, 5).
Ты привел примеры, у которых упорядоченная 5-ка совпадает.
А теперь забудь про неё, прочитай, что из себя представляет моя упорядоченная четверка и построй её для этих эллипсов.
Ты получишь (0, 0, 5, 6) и (0, 0, 6, 5).
С того, что эллипсы (0, 0, 5, 6, 0) и (0, 0, 6, 5, 90) совпадают как множества точек, а, следовательно, упомянутые тобой классы эллипсов пересекаются.
Отсюда я сделал вывод, что ты сравниваешь эллипсы не как множества точек.
Отсюда я сделал вывод, что ты сравниваешь эллипсы не как множества точек.
Я вообще-то привёл другие примеры.
Ты что, читать не умеешь? В каком месте совпадают вот эти пятёрки : (0, 0, 5, 6, 0) и (0, 0, 5, 6, 90)? Совпадают как раз четвёрки!
Какие четверки?
Да, извини, я не совсем то имел ввиду. Про равенство пятерок сказал хуйню.
Какие четверки?
Да, извини, я не совсем то имел ввиду. Про равенство пятерок сказал хуйню.
Какие четверки?
Что сразу порождает два непересекающихся класса эллипсов, подходящих под это утверждение - с углом поворота pi * n и с углом pi * n + pi / 2.Читай свои посты.
1-й эллипс. (0, 0, 2, 3, 0) - эллипс в классе с углом поворота pi*n (n = 0)
2-й эллипс. (0, 0, 3, 2, 90) - эллипс в классе с углом поворота p*n + pi/2 (n = 0)
Эти два эллипса совпадают как множества точек.
Следовательно твое утверждение о непересечении классов эллипсов неверно, либо ты рассматриваешь эллипсы не как мн-ва точек.
Если тебе сложно оперировать эллипсами с неравными осями, попробуй рассмотреть окружность
(0, 0, 2, 2, 0)
(0, 0, 2, 2, 90)
(0, 0, 2, 2, 0)
(0, 0, 2, 2, 90)
Милый дружок! Ты не представляешь даже, каких усилий мне стоит сдерживать матерные слова, которым, конечно же, не место в этом Храме Науки.
Ты только что задал произвольный эллипс пятью параметрами. Потом другой такой эллипс. Потом откусил последний параметр, и почему-то считаешь, что то, что ты получил, есть единственный способ задать эллипс-с-осями-параллельными-осям-координат четыремя параметрами. Это не так, милый мой дружочек.
Видишь ли, у меня есть алгоритм, позволяющий осуществить взаимно однозначное соответствие между множеством эллипсов-с-осями-параллельными-осям-координат и множеством кортежей из четырёх вещественных чисел, в которых третье и четвёртое - неотрицательные. Причём без всяких фокусов типа компрессии двух вещественных чисел в одно.
Сдаётся мне, все присутствующие (кроме тебя) его уже поняли. Тем не менее я предлагаю Спор. Я предоставляю тебе алгоритм в достаточно формальном виде, ты пытаешься найти контрпример, демонстрирующий отсутствие взаимно-однозначного отображения. Например эллипс-с-осями-параллельными-осям-координат, не задающий никакую такую четверку чисел, или две различные четвёрки чисел, задающих один и тот же эллипс, или два эллипса, задающих одну и ту же четверку чисел, или четверку чисел, не задающую ни один эллипс.
Если тебе это не удаётся в течение двух суток после опубликования мной алгоритма, ты покупаешь и приносишь мне одну полуторалитровую баклажку пива "Жигулёвское". Если тебе это удаётся, я покупаю и приношу тебе денежноэквивалентное количество пива или сока на твой выбор.
Ну?
Ты только что задал произвольный эллипс пятью параметрами. Потом другой такой эллипс. Потом откусил последний параметр, и почему-то считаешь, что то, что ты получил, есть единственный способ задать эллипс-с-осями-параллельными-осям-координат четыремя параметрами. Это не так, милый мой дружочек.
Видишь ли, у меня есть алгоритм, позволяющий осуществить взаимно однозначное соответствие между множеством эллипсов-с-осями-параллельными-осям-координат и множеством кортежей из четырёх вещественных чисел, в которых третье и четвёртое - неотрицательные. Причём без всяких фокусов типа компрессии двух вещественных чисел в одно.
Сдаётся мне, все присутствующие (кроме тебя) его уже поняли. Тем не менее я предлагаю Спор. Я предоставляю тебе алгоритм в достаточно формальном виде, ты пытаешься найти контрпример, демонстрирующий отсутствие взаимно-однозначного отображения. Например эллипс-с-осями-параллельными-осям-координат, не задающий никакую такую четверку чисел, или две различные четвёрки чисел, задающих один и тот же эллипс, или два эллипса, задающих одну и ту же четверку чисел, или четверку чисел, не задающую ни один эллипс.
Если тебе это не удаётся в течение двух суток после опубликования мной алгоритма, ты покупаешь и приносишь мне одну полуторалитровую баклажку пива "Жигулёвское". Если тебе это удаётся, я покупаю и приношу тебе денежноэквивалентное количество пива или сока на твой выбор.
Ну?
Серёжа, я говорю как раз про те эллипсы, у которых первые четыре параметра совпадают. А ты меня упорно не хочешь понимать, и говоришь про то, что (x, y, h, w, 0) и (x, y, w, h, 90) совпадают. Ясен хрен, что они совпадают, но я же не о них говорю.
Прочитал про окружность?
Да, вот ФЖ выше написал, что не совсем понятно, с чего ты взял, что чтобы получить нашу четверку из твоей пятерки, нужно отбросить последний элемент 5-ки.
Такого нигде не написано.
Такого нигде не написано.
ФЖ, наличие такого алгоритма (в котором я не сомневаюсь, заметь не имеет никакого отношения к тому, что фраза, из-за которой возник спор, была неточной.
Уточни фразу, пожалуйста, а то мы тут спорим чего-то.
Первая фраза на тему эллипса-с-осями-бла-бла-бла твоя.
Вот она:
Потому что параметра всего четыре.
Вот она:
Даже если одна ось вертикальна, то можно построить как минимум два разных эллипса с одинаковыми другими четырьмя параметрамиОна неверна.
Потому что параметра всего четыре.
Я сказал
Мне ответили
Вообще-то 4х параметров маловато для построения эллипса.С этим-то никто не будет спорить?
Мне ответили
автор трэда наверно имеет в виду что одна ось вертикальна.Я сказал
Даже если одна ось вертикальна, то можно построить как минимум два разных эллипса с одинаковыми другими четырьмя параметрами.Отвлечёмся от асбтрактных рассуждений, и скажите, что неверного в последней цитате?
В каком месте она неверна? Я уже два раза примел примеры несовпадающих сллипса. у которых первые четыре параметра совпадают.
Их всего четыре, дружёк.
Четыре.
Четыре.
Четыре.
Четыре.
Поэтому словосочетание "первые четыре параметра", хотя формально и корректно, но на деле совершенно бессмысленно.
ФЖ, вчитайся в эту фразу по слогам, если тебе трудно её воспринимать.
Эллипс можно однозначно задать пятью параметрами.Конечно, имеется ввиду, что полуоси не равны.
Если мы среди всех эллипсов, заданных пятью параметрами, выберем те, у которых оси параллельны осям координат, и у которых первые четыре параметра совпадают, то в выборке будет ровно два несовпадающих эллипса.
Эта фраза, конечно, верна.
Однако она не имеет никакого отношения к заданию эллипса-бла-бла-бла при помощи ЧЕТЫРЁХ параметров.
Вообще даже неудивительно что у тебя появляется неоднозначность - данные-то избыточные.
Однако она не имеет никакого отношения к заданию эллипса-бла-бла-бла при помощи ЧЕТЫРЁХ параметров.
Вообще даже неудивительно что у тебя появляется неоднозначность - данные-то избыточные.
Вообще-то 4х параметров маловато для построения эллипса.Для описания множества всех эллипсов с осями, параллельными осям координат, 4-х параметров достаточно.
Это мы тебе и пытаемся втолковать, только ты сопротивляешься.
И не надо цитаты в code пихать, страница разъезжается =)
Утираю пот со лба. Наконец-то я был понят!
Это я просто тэг код тестировал.
…До хрипоты спорили три хороших человека… Спорили о словах…
Оставить комментарий
Flack_bfsp
Вообще-то 4х параметров маловато для построения эллипса.