C++ Посоветуйте библиотеку [update]
метод гаусса полный или ленточный?
У меня сейчас полный.
Хочу поменять на любой итерационный метод.
Хочу поменять на любой итерационный метод.
Во, держи. эта, как её. MPL, во!
DGauss.h
DGauss.c
DGauss.h
/*
-----------------------------------------------------------------------------
The contents of this file are subject to the Mozilla Public License
Version 1.1 (the "License"); you may not use this file except in compliance
with the License. You may obtain a copy of the License at
http://www.mozilla.org/MPL/MPL-1.1.html
Software distributed under the License is distributed on an "AS IS" basis,
WITHOUT WARRANTY OF ANY KIND, either expressed or implied. See the License for
the specific language governing rights and limitations under the License.
The Initial Developer of the Original Code is:
Vasiliy Olekhov <olekhov att gmail dott com>
Copyright (c) 2002, 2009 Olekhov Vasiliy
All Rights Reserved.
Last Modified: 2004-03-24
-----------------------------------------------------------------------------}
*/
#ifndef __DGAUSS__
#define __DGAUSS__
/*
метод гаусса, приспособленный для решения систем с ленточными матрицами
коэффициенты задаются след. образом:
реальный вид матрицы параметр A
* * * d a b c * * * d a b c
* * e d a b c * * e d a b c
* f e d a b c * f e d a b c
g f e d a b c g f e d a b c
g f e d a b c ==> g f e d a b c
g f e d a b * g f e d a b *
g f e d a * * g f e d a * *
g f e d * * * g f e d * * *
коэффициенты, отмеченные "*", не используются.
в данном примере ширина диагонали равна 3, размерность матрицы - 8
*/
// С помощью этой функции можно легко адресовать элементы. IC=IndexConvert
// Использование: A[IC(i,j,D)]=...
int IC(int i,int j,int D);
int DiagGSolve(double *A,int N,int D,double *X,double *B);
// печатать матрицу в удобном виде
void PM(double *A,int N,int D,double *B);
#endif
DGauss.c
/*
-----------------------------------------------------------------------------
The contents of this file are subject to the Mozilla Public License
Version 1.1 (the "License"); you may not use this file except in compliance
with the License. You may obtain a copy of the License at
http://www.mozilla.org/MPL/MPL-1.1.html
Software distributed under the License is distributed on an "AS IS" basis,
WITHOUT WARRANTY OF ANY KIND, either expressed or implied. See the License for
the specific language governing rights and limitations under the License.
The Initial Developer of the Original Code is:
Vasiliy Olekhov <olekhov att gmail dott com>
Copyright (c) 2002, 2009 Olekhov Vasiliy
All Rights Reserved.
Last Modified: 2004-03-24
-----------------------------------------------------------------------------}
*/
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#ifndef min
#define min(a,b) ( (a)<(b)?(a):(b) )
#endif
#ifndef max
#define max(a,b) ( (a)>(b)?(a):(b) )
#endif
#include "DGauss.h"
int DiagGSolve(double *A,int N,int D,double *X,double *B)
{
int i,j,k;
double S;
// прямой ход
for(i=0;i<N-1;i++)
{
printf("%05d/%05d\r",i,N);
for(j=i+1;j<=min(i+D,N-1);j++)
{
S=A[IC(j,i,D)]/A[IC(i,i,D)]; A[IC(j,i,D)]=0;
for(k=i+1;k<=min(i+D,N-1);k++)
A[IC(j,k,D)]-=S*A[IC(i,k,D)];
B[j]-=S*B[i];
}
/*
printf("----------%d--------",i);
PM(A,N,D,B);
*/
}
// printf("туда\n");
// обратный ход
X[N-1]=B[N-1]/A[IC(N-1,N-1,D)];
for(i=N-2;i>=0;i--)
{
S=0;
for(j=i+1;j<min(i+1+D,N);j++)
S+=A[IC(i,j,D)]*X[j];
X[i]=(B[i]-S)/A[IC(i,i,D)];
}
return 0;
}
int IC(int i,int j,int D)
{
if(abs(i-j)>D)
{
printf("Index violation: |%d-%d|>%d\n",i,j,D);
exit(1);
}
// printf("good\n");
return ( (i)*(2*D+1)+j)-(i)+(D );
}
void PM(double *A,int N,int D,double *B)
{
int P;
char buf[1024];
int i,j;
printf(">>\n");
P=7;
for(i=0;i<N;i++)
{
sprintf(buf,"%%%ds",max(i-D,0)*P);
printf(buf,"");
for(j=0;j<2*D+1;j++)
{
if(j-D+i<max(i-D,0) || j-D+i>min(i+D,N-1 continue;
printf("%+6.2lf ",A[i*(2*D+1)+j]);
}
sprintf(buf,"%%%ds"N-min(i+D,N-1*P;
printf(buf,"");
printf("%+6.2le",B[i]);
printf("\n");
}
}
нафига итерационный?!
пример моих расчётов:
кол-во узлов: 47246
кол-во элементов-треугольников: 93690
кол-во сторон треугольников: 140935
матрица ленточная, ширина диагонали: 448.
т.е. расчёт ведётся не для матрицы 47к*47к, а для ленты 2*448*47к
время для одного рассчёта:
Work time: 0 hours 1 minutes 13 seconds
машина - http://parallel.ru/cluster/skif_msu.html
задача не распараллелена, используется только один процессор
на моём домашнем Q6600 думаю считалось бы минуты 4
кол-во узлов: 47246
кол-во элементов-треугольников: 93690
кол-во сторон треугольников: 140935
матрица ленточная, ширина диагонали: 448.
т.е. расчёт ведётся не для матрицы 47к*47к, а для ленты 2*448*47к
время для одного рассчёта:
Work time: 0 hours 1 minutes 13 seconds
машина - http://parallel.ru/cluster/skif_msu.html
задача не распараллелена, используется только один процессор
на моём домашнем Q6600 думаю считалось бы минуты 4
фрагмент моих элементов:

результаты расчётов:
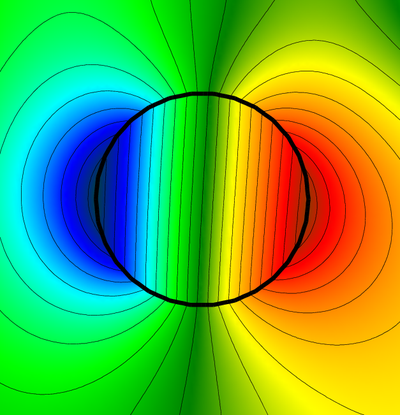

результаты расчётов:

на моём домашнем Q6600 думаю считалось бы минуты 4Думаешь ксеон на одном ядре сильно лучше квады на одном ядре?
Думаю, Зион 3ГГц с 3Мб кэша на ядро лучше, чем квад 2.4ГГц с 2Мб кэша на ядро.
и как бы шина у зиона быстрее. в 1.5 раза
и как бы шина у зиона быстрее. в 1.5 раза
Думаю, Зион 3ГГц с 3Мб кэша на ядро лучше, чем квад 2.4ГГц с 2Мб кэша на ядро.Но не в 4 же раза) Тем более на серверах стоит скорее всего более латентная память. Хотся сравнительных замеров! =)
и как бы шина у зиона быстрее. в 1.5 раза
параметры машинок:
Кластер:
железяку можно посмотреть по ссылке выше.
домашняя:
Q6600, 4x2GB DDR2, 800MHz, 4-4-4-12, GA-EP4-DS3.
Win2003 Server 32bit. (PAE, ага, 8гб все видятся )
)
два компилера:
и
Кластер:
[%username%@T60-2 ~]$ uname -a
Linux T60-2.parallel.ru 2.6.18-hpc-alt1.M41.1 SMP Fri Sep 26 13:28:44 MSD 2008 x86_64 GNU/Linux
[%username%@T60-2 ~]$ mpicc --version -v
mpicc for 1.2.7 (release) of : 2005/06/22 16:33:49
Version 11.0
icc (ICC) 11.0 20081105
Copyright (C) 1985-2008 Intel Corporation. All rights reserved.
железяку можно посмотреть по ссылке выше.
домашняя:
Q6600, 4x2GB DDR2, 800MHz, 4-4-4-12, GA-EP4-DS3.
Win2003 Server 32bit. (PAE, ага, 8гб все видятся
 )
)два компилера:
Open Watcom C/C++ CL Clone for 386 Version 1.7
Portions Copyright (c) 1995-2002 Sybase, Inc. All Rights Reserved.
Source code is available under the Sybase Open Watcom Public License.
See http://www.openwatcom.org/ for details.
и
Microsoft (R) 32-bit C/C++ Optimizing Compiler Version 15.00.30729.01 for 80x86
Copyright (C) Microsoft Corporation. All rights reserved.
через видеокарту считай
в CUDA в BLAS есть решение уравнений вида AX=B
в CUDA в BLAS есть решение уравнений вида AX=B
домашняя:
OpenWatcom: 08:10
Microsoft: 03:40
Кластер: 0:38

OpenWatcom: 08:10
Microsoft: 03:40
Кластер: 0:38

Уф, жестоко. Можешь кодом поделиться, у себя попробую?
А почему не используешь интеловский компилятор на домашней машине?
у меня на домашней машине "модельный" компилятор - OpenWatcom
домашняя машина у меня не счётная. мне скорости не важны.
icc ещё кстати циклы разворачивает - раза в четыре.
домашняя машина у меня не счётная. мне скорости не важны.
icc ещё кстати циклы разворачивает - раза в четыре.
я в этом полный профан
для меня "CUDA" и "BLAS" как иероглифы.
я молчу про "считать через видеокарту"
Дайте, пожалуйста, ссылку, где целиком описана одна библиотека - как готовить данные на вход, в каком формате выдается результат, ну и сама библиотека.
Например, как привести матрицу к ленточному виду.
для меня "CUDA" и "BLAS" как иероглифы.
я молчу про "считать через видеокарту"
Дайте, пожалуйста, ссылку, где целиком описана одна библиотека - как готовить данные на вход, в каком формате выдается результат, ну и сама библиотека.
Например, как привести матрицу к ленточному виду.
а у тебя разве матрица и так не ленточная получается?
оцени ширину ленты - по-моему это максимальная разница между индексами соседних узлов.
оцени ширину ленты - по-моему это максимальная разница между индексами соседних узлов.
Получается, что в случае 2D FE ширина ленты будет порядка N^{1/2}. А в случае 3D FE будет уже N^{2/3}. В то время как на самом деле в строке лишь десяток ненулевых элементов.
А это значит при реально больших N у нас не только расходуется лишняя память, но ещё и время…
Мне вот кажется здесь очень хорошо вписались бы разреженные матрицы и итерационные методы с правильно выбранными предобуславливателями. И время 1 минута для 47к вершин мне тоже кажется очень большим, тем более для такой мощной машины… Хотя, может это просто задачка такая. Я вот студентам даю лишь простые модельные задачки, на них и для сеточек с 64к вершин за секунды считается на обычном стареньком ноуте
А это значит при реально больших N у нас не только расходуется лишняя память, но ещё и время…
Мне вот кажется здесь очень хорошо вписались бы разреженные матрицы и итерационные методы с правильно выбранными предобуславливателями. И время 1 минута для 47к вершин мне тоже кажется очень большим, тем более для такой мощной машины… Хотя, может это просто задачка такая. Я вот студентам даю лишь простые модельные задачки, на них и для сеточек с 64к вершин за секунды считается на обычном стареньком ноуте

/*
метод гаусса, приспособленный для решения систем с ленточными матрицами
коэффициенты задаются след. образом:
реальный вид матрицы параметр A
* * * d a b c * * * d a b c
* * e d a b c * * e d a b c
* f e d a b c * f e d a b c
g f e d a b c g f e d a b c
g f e d a b c ==> g f e d a b c
g f e d a b * g f e d a b *
g f e d a * * g f e d a * *
g f e d * * * g f e d * * *
коэффициенты, отмеченные "*", не используются.
в данном примере ширина диагонали равна 3, размерность матрицы - 8
*/
если под ленточной сейчас подразумевается матрица, описанная выше, то нет
даже элементы на диагонали принимают разные значения
даже элементы на диагонали принимают разные значенияне, одинаковость элементов не связана с ленточностью
возможно, неточное определение:
"шириной" ленты является такое l = 2k+1, что для всех i < j - k и для всех i > j + k выполнено Aij = 0
Да, именно это и подразумевается. При таком подходе нумерация вершин значительно влияет на ширину ленты. И как следствие немаловажен предварительный процесс перенумерации вершин для уменьшения ширины ленты
я перенумерацию вершин делаю. именно поэтому ширина ленты составляет 1-2% от размерности.
сколько диагоналей у матрицы на 64к элементов? если три - то LU-разложение всяко быстрее будет, чем итерационные методы.
А если размерность 64к, а ширина ленты 600 - тогда как? думаю, не так уж и быстр окажется итерационный метод.
у меня под шириной ленты подразумевается число k из поста , т.е. реальная ширина ленты 2*k+1
сколько диагоналей у матрицы на 64к элементов? если три - то LU-разложение всяко быстрее будет, чем итерационные методы.
А если размерность 64к, а ширина ленты 600 - тогда как? думаю, не так уж и быстр окажется итерационный метод.
у меня под шириной ленты подразумевается число k из поста , т.е. реальная ширина ленты 2*k+1
Там были ячейки – квадраты, сетка структурированная. Шаблон – пятиточечный. То есть в строке не больше пяти ненулевых элементов. Всего в матрице ненулевых диагоналей 5. Но расстояние между ними порядка n. То есть если её рассматривать как ленточную, то будет она ширины 2n+1 и почти вся забита нулями.
С трёхдиагональными матрицами очевидно можно методом прогонки за O(n) решить. Но такое скорее только на одномерных задачках встречается.
В итерационных методах ширина ленты вообще не важна, если использовать эффективное хранение разреженной матрицы. Там важно количество ненулевых элементов. А их порядка 5n (7n в 3D) для квадратов. Для других типов сеток константы другие, но тоже не фатальные.
Upd: да, в МКЭ всё же 9 ненулевых в строке на плоской сетке. Это я для МКР/МКО приводил пример. Уравнение – конвекция диффузия, нестационарная
С трёхдиагональными матрицами очевидно можно методом прогонки за O(n) решить. Но такое скорее только на одномерных задачках встречается.
В итерационных методах ширина ленты вообще не важна, если использовать эффективное хранение разреженной матрицы. Там важно количество ненулевых элементов. А их порядка 5n (7n в 3D) для квадратов. Для других типов сеток константы другие, но тоже не фатальные.
Upd: да, в МКЭ всё же 9 ненулевых в строке на плоской сетке. Это я для МКР/МКО приводил пример. Уравнение – конвекция диффузия, нестационарная
ок, согласен. у меня количество ненулевых элементов в строке колеблется от 4 до 8.
к тому же в полосе ненулевые элементы распределены условно хаотично.
в общем, я выбрал именно такую реализацию.
могу сдампить матрицу (не всю, а только ленту ) и попробовать скормить её итерационному методу - и сравнить результаты..
) и попробовать скормить её итерационному методу - и сравнить результаты..
к тому же в полосе ненулевые элементы распределены условно хаотично.
в общем, я выбрал именно такую реализацию.
могу сдампить матрицу (не всю, а только ленту
 ) и попробовать скормить её итерационному методу - и сравнить результаты..
) и попробовать скормить её итерационному методу - и сравнить результаты..update: начальство требует итерационный метод решения СЛУ
Оставить комментарий
Robert08
Есть собственный код, 2D FE, система линейных уравнений решается методом Гаусса. Хочу сделать апгрейд, чтобы уменьшить время вычисления.Посоветуйте, пожалуйста, библиотеку с функциями чтобы можно было заменить решение системы линейных уравнений или вообще весь конечно-элементный блок.
updated:
нужен итеративный метод
Из того, что я прочитала, наверное, хорошо бы GMRES.
И, пожалуйста, научите пользоваться.