Алгоритм определения находится ли точка внутри множества точек?
Вначале строишь выпуклую оболочку - это будет множество плоскостей. Затем для проверяемой точки проверяешь чтобы она лежала по определенную сторону от каждой плоскости. Для этого надо в уравнение плоскости подставить координаты точки и сравнить получившееся число с 0.
Ты уверен, что именно в таком виде это будет работать? 
Вначале строишь выпуклую оболочку - это будет множество плоскостей.можно поподробней?
в смысле, как ее строить?
Ага.
Что именно поподробнее? Как строить?
бля, я как раз подредактировал 
Нужно брать не просто уравнения плоскостей, а уравнения ориентированных плоскостей.
Например строя плоскости по трем точкам A, B, C через определитель, нужно брать их в такой последовательности, чтобы обход {A, B, C} был против часовой стрелки, если смотреть снаружи поверхности.
А без этой добавки пахать не будет
Например строя плоскости по трем точкам A, B, C через определитель, нужно брать их в такой последовательности, чтобы обход {A, B, C} был против часовой стрелки, если смотреть снаружи поверхности.
А без этой добавки пахать не будет
в смысле, как ее строить?Ну вот это как раз надо в инете искать. Известны алгоритмы со сложностью (n ln n) - от количества точек.
Ну например так(я не уверен что это оптимальный алгоритм, и что он вообще правильный ) :
1) Находишь точку с наименьшей координатой x
2) Проводишь через нее плоскость, параллельную oYZ. Находишь 2(или более) точки с наименьшим углом отклонения от этой плоскости(с началом угла в точке из пункта 1). Строишь через эти точки плоскость. Это и будет одна из плоскостей. Вычеркиваешь точки из списка.
3) Для полученной плоскости и лежащих на ней точек из плоскости применяешь процедуру 2. И так далее.
) :1) Находишь точку с наименьшей координатой x
2) Проводишь через нее плоскость, параллельную oYZ. Находишь 2(или более) точки с наименьшим углом отклонения от этой плоскости(с началом угла в точке из пункта 1). Строишь через эти точки плоскость. Это и будет одна из плоскостей. Вычеркиваешь точки из списка.
3) Для полученной плоскости и лежащих на ней точек из плоскости применяешь процедуру 2. И так далее.
А я так и сказал. Заметь, я говорил про знак. А не про больше/меньше 0. Вначале конечно надо взять пробную точку и если что умножить уравнение плоскости на -1.
2) Проводишь через нее плоскость, параллельную oYZ. Находишь 2(или более) точки с наименьшим углом отклонения от этой плоскости(с началом угла в точке из пункта 1). Строишь через эти точки плоскость. Это и будет одна из плоскостей. Вычеркиваешь точки из списка.Да нет, неправильно, нет у тебя трехмерного воображения
нихуя не понял, честно говоря =)
воспользуюсь советом
воспользуюсь советом
А чего не так? 
x = (0,0,0)
y = (0,1,0)
z = (0,-1,0)
a = (10,0,1)
b = (10,0,-1)
y и z - имеют наименьший угол (потому что 10 - много но плоскость xyz горизонтальная и a и b по разные стороны от нее.
y = (0,1,0)
z = (0,-1,0)
a = (10,0,1)
b = (10,0,-1)
y и z - имеют наименьший угол (потому что 10 - много но плоскость xyz горизонтальная и a и b по разные стороны от нее.
Через xyz проходит сколь угодно много плоскостей Поэтому нужно взять еще одну точку. просто я не описал вырожденные случаи, там должно быть понятно что делать
Поэтому нужно взять еще одну точку. просто я не описал вырожденные случаи, там должно быть понятно что делать Про одинаковый знак понятно.
Придется объяснить подробней. Если одновременно во всех уравнениях ax+by+cz+d=0 вектор {a, b, c} будет определять внешнюю (или одновременно во всех внутреннюю) нормаль, то это будет работать, а если нет – не будет!
Придется объяснить подробней. Если одновременно во всех уравнениях ax+by+cz+d=0 вектор {a, b, c} будет определять внешнюю (или одновременно во всех внутреннюю) нормаль, то это будет работать, а если нет – не будет!
Чо, в трёхмерном пространстве за O(n ln n) ? 
Вообще, если свободного времени много (например 3-й курс то самому придумать и закодировать - бесценное упражнение. Но начать лучше с двумерного случая, чтобы представить себе что к чему... Если интересно, могу помочь советами , в свое время я тоже об этом думал.
то самому придумать и закодировать - бесценное упражнение. Но начать лучше с двумерного случая, чтобы представить себе что к чему... Если интересно, могу помочь советами , в свое время я тоже об этом думал.Блин. Еще раз: у нас есть пробная точка, которая точно лежит внутри. Знаки для пробной точки и для проверяемой точки должны совпадать. Но это не значит что они совпадают для всех плоскостей сразу. Поэтому нормали могут быть направлены как внутрь, так и наружу.
двумерный - это просто, еще в 10-ом классе проходили =)
для трехмерного за N^4 очевидный алгоритм, даже думать не надо =)
более быстрые, пожалуй, реально в инете поищу
для трехмерного за N^4 очевидный алгоритм, даже думать не надо =)
более быстрые, пожалуй, реально в инете поищу
Хе-хе, я тебя понял.
Ну тогда у тебя надо помнить ориентацию каждой плоскости – по биту на штуку
Ну тогда у тебя надо помнить ориентацию каждой плоскости – по биту на штуку
Ну вот чего ты говоришь? 
Какие нафиг вырожденные случаи? Картинку что ли нарисуй... Ладно, щас сам нарисую
Какие нафиг вырожденные случаи? Картинку что ли нарисуй... Ладно, щас сам нарисую a и b - обе там же, где и c, но одна "над" экраном, а другая "под".
ось OY
^
| y
|
x-----------------------с----------------------> ось OX
|
| z
Да... Что-то не то получается... Надо подумать
в трёхмерном пространстве за O(n ln n)ну там основная идея, что можно за почти линейное время разделить все точки на 3 кучки, чтобы выпуклая оболочка 1-ой не пересекалась с выпуклой оболочкой 3-ей, причем в них примерно одинаковое количество точек, а 2-ая кучка - "маленькая" (пограничная
). Дальше для 1,3 оболочки рекурсивно строятся, а потом все это соединяется тоже за почти линейное время. Пишу "почти линейное" потому что не помню линейное оно там или нет, кажись не линейное, но меньше n ln n .Умеют даже за O(n ln h где h - количество точек оболочки.
Например: http://citeseer.ist.psu.edu/chan95outputsensitive.html
Например: http://citeseer.ist.psu.edu/chan95outputsensitive.html
Ок спасибо. Попробую запрогать кукхалл.
можно вопрос?
вот такое множество ограничится
так:
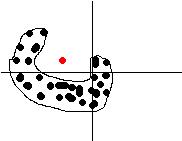
или так:
?
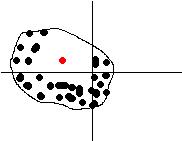
вот такое множество ограничится
так:
или так:
?
если второй, то почему бы
не взять за начало отсчета искомую точку, пересчитать все координаты относительно её, одновременно определяя в какой четеврти они находятся. если все в одной полуплоскости то не попадает, если нет, то попадает
не взять за начало отсчета искомую точку, пересчитать все координаты относительно её, одновременно определяя в какой четеврти они находятся. если все в одной полуплоскости то не попадает, если нет, то попадает
Второе.
т.к. обычно нужна выпуклая оболочка.
т.к. обычно нужна выпуклая оболочка.
тогда, что думаете по моему варианту?
что выше
что выше
ниче не говорите понял что чушь
хотя если апргейтнуть проверкой всех полуплоскостей...
если все в одной полуплоскости тоЭто правильно, но как ты это будешь определять, я не понял.
одновременно определяя в какой четевртиУж четверти тут вообще ни при чем...
Ты хочешь найти не выпуклую границу семейства точек? Есть кажись алгоритм Marching cubes... Не помню что и как но есть!
Допустим, что мы уже построили выпуклую оболочку для множества точек.
Тогда вот два алгоритма проверки, находится ли точка внутри выпуклой оболочки:
1. Проверить, что нормали ко всем плоскостям направлены в сторону от искомой точки.
Здесь проблема в том, что хз, как посчитать нормали. Проблема решается так:
Выбираются два сопряженных многоугольника, потом в каждой плоскости строится единичный вектор, перпендикулярный общему ребру. Далее косинусы углов между суммой этих перпендикуляров и каждой из нормалей к граням должны совпадать по знаку. Если не совпадают, то одна из нормалей домножатается на -1. Так для всех граней.
2. провести любую прямую через искомую точку. Если точка внутри оболочки, то она пересечет его ровно два раза. При этом вектора, направленные из искомой точки в точки пересечений имеют разные знаки. По-моему этот способ проще, чем первый
Тогда вот два алгоритма проверки, находится ли точка внутри выпуклой оболочки:
1. Проверить, что нормали ко всем плоскостям направлены в сторону от искомой точки.
Здесь проблема в том, что хз, как посчитать нормали. Проблема решается так:
Выбираются два сопряженных многоугольника, потом в каждой плоскости строится единичный вектор, перпендикулярный общему ребру. Далее косинусы углов между суммой этих перпендикуляров и каждой из нормалей к граням должны совпадать по знаку. Если не совпадают, то одна из нормалей домножатается на -1. Так для всех граней.
2. провести любую прямую через искомую точку. Если точка внутри оболочки, то она пересечет его ровно два раза. При этом вектора, направленные из искомой точки в точки пересечений имеют разные знаки. По-моему этот способ проще, чем первый
Насколько я понимаю то, что я прочитал по данным мне ссылкам (да собственно я это и предполагал с самого начала) труднее всего именно построить выпуклую оболочку. По ссылке есть только один алгоритм, для 3-х мерного случая.
>1. Проверить, что нормали ко всем плоскостям направлены в сторону от искомой точки.
>Здесь проблема в том, что хз, как посчитать нормали. Проблема решается так:
>Выбираются два сопряженных многоугольника, потом в каждой плоскости строится единичный вектор, >перпендикулярный общему ребру. Далее косинусы углов между суммой этих перпендикуляров и каждой из >нормалей к граням должны совпадать по знаку. Если не совпадают, то одна из нормалей домножатается >на -1. Так для всех граней.
ну это писец какойто
>2. провести любую прямую через искомую точку. Если точка внутри оболочки, то она пересечет его >ровно два раза. При этом вектора, направленные из искомой точки в точки пересечений имеют разные >знаки. По-моему этот способ проще, чем первый
Это выходит провести прямую, я для всех граней оболочки (пусть даже скажем треугольных проверять (решать нелинейное уравнение) где пересекается эта прямая с этой гранью. Если пересекается (она будет пересекаться в 100 % без малого случаях прооверять, находится ли точкка пересечения внутри грани или за пределами. И так по всем граням. Ну да алгоритм верный. Только совсем не целесообразный.
Вобщем все равно, если строишь выпуклую оболочку - проще сразу создать уравнения для всех граней в виде ax by cz d так, чтобы весь многогранник находился по положительную полуплоскость от грани, а при проверке, находится ли точка внутри выпуклой оболочки - проверять, чтобы для всех граней ax1 by1 cz1 d был > 0; Вобщем это похоже на алгоритм 1, но только без гемора типо сторить какието нормали.
А второй алгоритм, кстати подойдет для определения, находится ли точка внутри любого многогранника, не обязательно выпуклого.
з.ы. исправил встретившееся "многоугольник" на "многогранник"
>1. Проверить, что нормали ко всем плоскостям направлены в сторону от искомой точки.
>Здесь проблема в том, что хз, как посчитать нормали. Проблема решается так:
>Выбираются два сопряженных многоугольника, потом в каждой плоскости строится единичный вектор, >перпендикулярный общему ребру. Далее косинусы углов между суммой этих перпендикуляров и каждой из >нормалей к граням должны совпадать по знаку. Если не совпадают, то одна из нормалей домножатается >на -1. Так для всех граней.
ну это писец какойто
>2. провести любую прямую через искомую точку. Если точка внутри оболочки, то она пересечет его >ровно два раза. При этом вектора, направленные из искомой точки в точки пересечений имеют разные >знаки. По-моему этот способ проще, чем первый
Это выходит провести прямую, я для всех граней оболочки (пусть даже скажем треугольных проверять (решать нелинейное уравнение) где пересекается эта прямая с этой гранью. Если пересекается (она будет пересекаться в 100 % без малого случаях прооверять, находится ли точкка пересечения внутри грани или за пределами. И так по всем граням. Ну да алгоритм верный. Только совсем не целесообразный.
Вобщем все равно, если строишь выпуклую оболочку - проще сразу создать уравнения для всех граней в виде ax by cz d так, чтобы весь многогранник находился по положительную полуплоскость от грани, а при проверке, находится ли точка внутри выпуклой оболочки - проверять, чтобы для всех граней ax1 by1 cz1 d был > 0; Вобщем это похоже на алгоритм 1, но только без гемора типо сторить какието нормали.
А второй алгоритм, кстати подойдет для определения, находится ли точка внутри любого многогранника, не обязательно выпуклого.
з.ы. исправил встретившееся "многоугольник" на "многогранник"
Сразу видно, что человек никогда реально подобной задачи не решал.
Вобщем все равно, если строишь выпуклую оболочку - проще сразу создать уравнения для всех граней в виде ax by cz d так, чтобы весь многоугольник находился по положительную полуплоскость от грани, а при проверке, находится ли точка внутри выпуклой оболочки - проверять, чтобы для всех граней ax1 by1 cz1 d был > 0; Вобщем это похоже на алгоритм 1, но только без гемора типо сторить какието нормали.
Допустим, у нас единичный куб в первом октанте.
У него есть две грани, заданные так: x = 0 ; x -1 = 0;
Подставляем точку x=0.5, y=0.5, z=0.5.
что получаем?
0.5 >0;
0.5-1 < 0
То есть точка лежит вне куба, что неверно.
Алгоритм же, работающий с нормалями такую проверку проходит .
> У него есть два ребра, заданные так: x = 0 ; x -1 = 0;
При чем здесь ребра?
Речь изначально шла про плоскости на которых лежат грани.
При чем здесь ребра?
Речь изначально шла про плоскости на которых лежат грани.
При чем здесь ребра?Очепятка
Речь изначально шла про плоскости на которых лежат грани.
многоугольник находился по положительную полуплоскость от граниСоответственно грани для такого куба будут:
x = 0
и
1 - x = 0
Соответственно грани для такого куба будут:Гениально! А теперь докажи это компьютеру!
x = 0
и
1 - x = 0
Если правильно строить выпуклую оболочку, то так и будет получаться.
Сразу видно, что человек никогда реально подобной задачи не решал.Бляааааааааа
Если правильно строить выпуклую оболочку, то так и будет получаться.Да. если строить ее так, чтобы коэффициенты A, B, C уравнений плоскостей соответствовали нормалям к этим плоскостям, направленным ОТ внутренней части многогранника
Зкб.
У единичнного куба в первом октанте такие уравнения граней (всего 6)
x=0
1-x=0
y=0
1-y=0
z=0
1-z=0
Хочешь сказать, что условию
(x>0) && (1-x>0) && (y>0) && (1-y>0) && (z>0) && (1-z>0)
удовлетворяют какието точки вне куба? или какието точки, не удовлетворяющие этому условию лежат внутри?
(про > Или >= я не говорю, вопрос про границы пусть каждый решает сам)
и не надо никаких нормалей и косинусов. Один раз вычислил значения a, b, c, d для каждой грани, и после этого можешь хоть 100 раз проверять, находится ли точка внутри выпуклой оболочки. Помоему с вычислительной точки зрения - выгодно. Вычисления все первого порядка.
У единичнного куба в первом октанте такие уравнения граней (всего 6)
x=0
1-x=0
y=0
1-y=0
z=0
1-z=0
Хочешь сказать, что условию
(x>0) && (1-x>0) && (y>0) && (1-y>0) && (z>0) && (1-z>0)
удовлетворяют какието точки вне куба? или какието точки, не удовлетворяющие этому условию лежат внутри?
(про > Или >= я не говорю, вопрос про границы пусть каждый решает сам)
и не надо никаких нормалей и косинусов. Один раз вычислил значения a, b, c, d для каждой грани, и после этого можешь хоть 100 раз проверять, находится ли точка внутри выпуклой оболочки. Помоему с вычислительной точки зрения - выгодно. Вычисления все первого порядка.
> Гениально! А теперь докажи это компьютеру!
Можно поступить просто: руками указываешь программе точку внутри многогранника - и программа сама расставит все знаки
можно тоже самое сделать и автоматически - через определение углов между плоскостями.
Можно поступить просто: руками указываешь программе точку внутри многогранника - и программа сама расставит все знаки
можно тоже самое сделать и автоматически - через определение углов между плоскостями.
>Да. если строить ее так, чтобы коэффициенты A, B, C уравнений плоскостей соответствовали нормалям к этим плоскостям, направленным ОТ внутренней части многогранника
А я что написал:
>Вобщем все равно, если строишь выпуклую оболочку - проще сразу создать уравнения для всех граней в виде ax by cz d так, чтобы весь многоугольник находился по положительную полуплоскость от грани, а при проверке, находится ли точка внутри выпуклой оболочки - проверять, чтобы для всех граней ax1 by1 cz1 d был > 0; Вобщем это похоже на алгоритм 1, но только без гемора типо сторить какието нормали.
подчеркиваю:
>многоугольник находился по положительную полуплоскость
А я что написал:
>Вобщем все равно, если строишь выпуклую оболочку - проще сразу создать уравнения для всех граней в виде ax by cz d так, чтобы весь многоугольник находился по положительную полуплоскость от грани, а при проверке, находится ли точка внутри выпуклой оболочки - проверять, чтобы для всех граней ax1 by1 cz1 d был > 0; Вобщем это похоже на алгоритм 1, но только без гемора типо сторить какието нормали.
подчеркиваю:
>многоугольник находился по положительную полуплоскость
Оставить комментарий
vertyal17
Т.е. задача: есть множество точек x[ i ],y[ i ],z[ i ] (коорд. i-й точки если на него снаружи какбы "натянуть" поверхность, получится выпуклый многогранник. Есть ли какойто алгоритм, определяющий находится ли точка с координатами x,y,z внутри этого многогранника?Понятно, что можно перебирать все внутренние тэтраэдеры в множестве, и проверять на то, что х,у,z находится внутри. Можно даже из множества x[ i ],y[ i ],z[ i ] както повыкидывать "внутренние" точки, но я думаю к такой задаче давно есть эффективный алгоритм. Где можно найти ? или может кто знает
зы. Не знаю как вышло что текст курсивом...