Аргументы в пользу состояния из MIT-овского учебника
А дальше ты читал?
нет еще, но пролистал. Да, они говорят, что за это приходится платить. Но совсем хорошего решения я дальше не нашел, ты нашел?
(define (estimate-pi trials)Через серию простых шагов этот код переписывается вот так:
(sqrt (/ 6 (random-gcd-test trials random-init))))
(define (random-gcd-test trials initial-x)
(define (iter trials-remaining trials-passed x)
(let ((x1 (rand-update x)))
(let ((x2 (rand-update x1)))
(cond ((= trials-remaining 0)
(/ trials-passed trials))
((= (gcd x1 x2) 1)
(iter (- trials-remaining 1)
(+ trials-passed 1)
x2))
(else
(iter (- trials-remaining 1)
trials-passed
x2))))))
(iter trials 0 initial-x))
static double estimate_pi(int trials)
{
return Math.Sqrt(6 / random_gcd_test(trials, cesaro_test()));
}
const int random_init = 0;
static Experiment cesaro_test(int x = random_init)
{
return () => {
var x1 = rand_update(x);
var x2 = rand_update(x1);
return Tuple.Create(gcd(x1, x2) == 1, cesaro_test(x2));
};
}
delegate Tuple<bool, Experiment> Experiment();
static double random_gcd_test(int trials, Experiment experiment)
{
return random_gcd_test_iter(trials, experiment, trials, 0);
}
static double random_gcd_test_iter(int trials, Experiment experiment,
int trials_remaining, int trials_passed)
{
if (trials_remaining == 0)
return (double) trials_passed/trials;
var tuple = experiment();
if (tuple.Item1)
return random_gcd_test_iter(trials, tuple.Item2, trials_remaining - 1, trials_passed + 1);
else
return random_gcd_test_iter(trials, tuple.Item2, trials_remaining - 1, trials_passed);
}
Теперь есть полное основание функцию random_gcd_test переименовать в monte_carlo, поскольку теперь это общий метод для алгоритма Монте-Карло.
P.S. можно не выеживаться и оставить Experiment интерфейсом, а не делегатом. Ну это я так, чтобы строчек меньше было.
В этом коде ты уже переизобрёл то что у них называется стримы (ленивые списки, в сущности; раздел 3.5), но ещё не дошёл до средств их композиции. Например, у тебя в cesaro_test жёстко зашито какой ГСЧ используется.
Например, у тебя в cesaro_test жёстко зашито какой ГСЧ используется.Если ГСЧ надо вынести как параметр, то это делается элементарно:
static double estimate_pi(int trials)
{
return Math.Sqrt(6 / random_gcd_test(trials, cesaro_test(rand())));
}
const int random_init = 0;
static Chain<int> rand(int x = random_init)
{
return () => Tuple.Create(x, rand(rand_update(x)));
}
static Chain<bool> cesaro_test(Chain<int> rand)
{
return () => {
var tuple1 = rand();
var tuple2 = tuple1.Item2();
return Tuple.Create(gcd(tuple1.Item1, tuple2.Item1) == 1, cesaro_test(tuple2.Item2));
};
}
delegate Tuple<T, Chain<T>> Chain<T>();
static double random_gcd_test(int trials, Chain<bool> experiment)
{
return random_gcd_test_iter(trials, experiment, trials, 0);
}
static double random_gcd_test_iter(int trials, Chain<bool> experiment,
int trials_remaining, int trials_passed)
{
if (trials_remaining == 0)
return (double)trials_passed / trials;
var tuple = experiment();
if (tuple.Item1)
return random_gcd_test_iter(trials, tuple.Item2, trials_remaining - 1, trials_passed + 1);
else
return random_gcd_test_iter(trials, tuple.Item2, trials_remaining - 1, trials_passed);
}
Можно еще обобщить. Рекурсивное обращение функций rand и random_gcd_test тоже можно вынести в общую функцию:
delegate Tuple<T, Chain<T>> Chain<T>();
static class ChainExtensions
{
public static Chain<TResult> Chain<T, TResult>(this T arg, Func<T, Tuple<TResult, T>> func)
{
return () => {
var tuple = func(arg);
return Tuple.Create(tuple.Item1, Chain(tuple.Item2, func));
};
}
}
static double estimate_pi(int trials)
{
return Math.Sqrt(6/random_gcd_test(
trials,
random_init.Chain(x => Tuple.Create(x, rand_update(x))).Chain(rand => {
var tuple1 = rand();
var tuple2 = tuple1.Item2();
return Tuple.Create(gcd(tuple1.Item1, tuple2.Item1) == 1, tuple2.Item2);
})));
}
const int random_init = 0;
static double random_gcd_test(int trials, Chain<bool> experiment)
{
return random_gcd_test_iter(trials, experiment, trials, 0);
}
static double random_gcd_test_iter(int trials, Chain<bool> experiment,
int trials_remaining, int trials_passed)
{
if (trials_remaining == 0)
return (double)trials_passed / trials;
var tuple = experiment();
if (tuple.Item1)
return random_gcd_test_iter(trials, tuple.Item2, trials_remaining - 1, trials_passed + 1);
else
return random_gcd_test_iter(trials, tuple.Item2, trials_remaining - 1, trials_passed);
}
С одной стороны, да, Chain похож на потоки. Я нашел раздел, где они переписывают этот же алгоритм через потоки. Спасибо.

Но с другой стороны, вынесенный в сабж вопрос, по сути, остается. У них позиция такая. Объекты дают модульность, но расплачиваемся состоянием. Потоки не имеют состояния, но плохо сочетаются с императивным стилем, например, Exercise 3.51.
Однако Chain родилась из кода в императивном стиле. Рождение произошло через последовательность элементарных шагов Extract Method и Introduce Parameter (чуть позже распишу подробно шаги с самого начала от первоначальной функции random_gcd_test). Пока не могу понять, как нечто, рожденное всего лишь как последовательность Extract Method и Introduce Parameter, может плохо сочетаться с императивным стилем? Может Chain это не потоки? По поводу Exercise 3.51, распечатка Chain производится элементарно через императивный стиль:
var chain = random_init.Chain(x => Tuple.Create(x, rand_update(x)));
for (var i = 0; i < 10; i++)
{
var tuple = chain();
Console.WriteLine(tuple.Item1);
chain = tuple.Item2;
}
В этом коде ты уже переизобрёл то что у них называется стримы (ленивые списки, в сущности; раздел 3.5), но ещё не дошёл до средств их композиции.Всё же Chain это не поток. Есть только некоторые сходства. Chain, как и написано, это делегат. Ни больше, ни меньше.
delegate Tuple<T, Chain<T>> Chain<T>();
Например, нет пустого потока как у них:
There is a distinguishable object, the-empty-stream, which cannot be the result of any cons-stream operation, and which can be identified with the predicate stream-null?
http://mitpress.mit.edu/sicp/full-text/book/book-Z-H-24.html...
Конечные Chain-ы реализуются естественным образом через Option type:
static Chain<Option<int>> enumerate_interval(int low, int high)
{
return low.Chain(x => Tuple.Create(x <= high ? x : Option<int>.None, x + 1));
}
Как они сами пишут, у потоков возникают дополнительные проблемы в императивном окружении. В то время как Chain это плоть от плоти императивная сущность, и естественным образом ведет себя в императивном окружении. При этом Chain, как и потоки, позволяет достичь модульности без mutable объектов.
Наверняка про Chain уже где-нибудь написано, вопрос, как это загуглить? Или мне дописывать еще одни подраздел про модульность в MIT-овский учебник?

Гугли codata и co-inductive types. Твой chain - как раз правильный поток, а вот "пустой поток" существовать не должен по-хорошему. Негоже путать инициальные алгебры (данные) и терминальные коалгебры (коданные).
Не, подожди, косписок, т.е. ко-"List a = Nul | Cons a (List a)", может быть как конечным, так и бесконечным; другое дело что бесконечный список "InfiniteList a = Cons a (InfiniteList a)" реализуется только в "ко" формализме (потому что понятно, как его деконструировать, но непонятно, как конструировать).
Да, верно. Собственно, второе - как раз классический стрим из всех статей про коданные.
В этом коде ты уже переизобрёл то что у них называется стримы (ленивые списки, в сущности; раздел 3.5), но ещё не дошёл до средств их композиции.MIT-вские потоки оказываются потребляют память пропорционально n. Об этом косвенно говорит вот такая странная реализация random-numbers:
(define random-numbers
(cons-stream 1
(stream-map rand-update random-numbers)))
Более естественная реализация была бы через самоссылающуюся функцию аналогичную map-successive-pairs.
Замеры также подтверждают, что память растет:
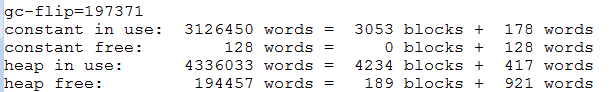
В тоже время через Chain можно сделать поточную запись как у них:
public static void Main()
{
Console.WriteLine(monte_carlo(cesaro_stream())
.Select(p => Math.Sqrt(6/p))
.Skip(10000000 - 1)().Item1);
}
static Chain<int> random_numbers()
{
const int random_init = 0;
return random_init.Chain(seed => Tuple.Create(seed, rand_update(seed)));
}
static Chain<bool> cesaro_stream()
{
return random_numbers().Chain(seed => {
var tuple1 = seed();
var tuple2 = tuple1.Item2();
return Tuple.Create(gcd(tuple1.Item1, tuple2.Item1) == 1, tuple2.Item2);
});
}
static Chain<double> monte_carlo(Chain<bool> experiment)
{
return new {experiment, passed = 0, failed = 0}.Chain(seed => {
int passed;
int failed;
var tuple = seed.experiment();
if (tuple.Item1)
{
passed = seed.passed + 1;
failed = seed.failed;
}
else
{
passed = seed.passed;
failed = seed.failed + 1;
}
return Tuple.Create((double) passed/(passed + failed), new {experiment = tuple.Item2, passed, failed});
});
}
delegate Tuple<T, Chain<T>> Chain<T>();
static class ChainExtensions
{
public static Chain<TResult> Chain<T, TResult>(this T arg, Func<T, Tuple<TResult, T>> func)
{
return () => {
var tuple = func(arg);
return Tuple.Create(tuple.Item1, Chain(tuple.Item2, func));
};
}
public static Chain<TResult> Select<TSource, TResult>(this Chain<TSource> it, Func<TSource, TResult> selector)
{
return it.Chain(chain => {
var tuple = chain();
return Tuple.Create(selector(tuple.Item1), tuple.Item2);
});
}
public static Chain<TSource> Skip<TSource>(this Chain<TSource> it, int count)
{
while (count > 0)
{
it = it().Item2;
--count;
}
return it;
}
}
Тут расход памяти и cpu такой же как при обычном императивном цикле.
 Просто этот цикл вынесен в общий метод Skip.
Просто этот цикл вынесен в общий метод Skip.Короче в MIT-овском учебнике явно налажали. Нет ни какой разницы между императивным стилем и stream-овым.
We began this chapter with the goal of building computational models whose structure matches our perception of the real world we are trying to model. We can model the world as a collection of separate, time-bound, interacting objects with state, or we can model the world as a single, timeless, stateless unity. Each view has powerful advantages, but neither view alone is completely satisfactory. A grand unification has yet to emerge. 76
http://mitpress.mit.edu/sicp/full-text/book/book-Z-H-24.html...
Великое объединение (grand unification) еще не наступило. Лол
 , какое нах объединение. Используйте Chain, и не будет разъединения. Писать можно как хочешь, можно рекурсией, можно корекурсией, можно циклом.
, какое нах объединение. Используйте Chain, и не будет разъединения. Писать можно как хочешь, можно рекурсией, можно корекурсией, можно циклом.А вот это вообще полный лол, обычные callback-и это квантовая механика не иначе:
Видимо, ООП головного мозга это, действительно, fundamental epistemological issues.
The object model approximates the world by dividing it into separate pieces. The functional model does not modularize along object boundaries. The object model is useful when the unshared state of the ``objects'' is much larger than the state that they share. An example of a place where the object viewpoint fails is quantum mechanics, where thinking of things as individual particles leads to paradoxes and confusions. Unifying the object view with the functional view may have little to do with programming, but rather with fundamental epistemological issues.

codataChain оказалась забавной штукой. С одной стороны интуитивно она напоминает generator-ы через yield. С другой стороны есть приятные отличия. Например, реализация факториала (или monte_carlo) через yield обладает mutable состоянием (переменные n и fac изменяются):
def faclist():
n = 0
fac = 1
while True:
yield fac
n += 1
fac *= n
This generates an infinite list of the factorials in order; a finite list can be produced by:
def faclist(k):
n = 0
fac = 1
while (n <= k):
yield fac
n += 1
fac *= n
http://en.wikipedia.org/wiki/Corecursion#Factorial
В случае Chain в алгоритме факториала (или monte_carlo) изменяемого состояния нет. К тому же нет необходимости разделять infinite list и finite list:
static void Main()
{
Console.WriteLine(faclist().Skip(5)().Item1);
}
static Chain<int> faclist()
{
return new {n = 0, fac = 1}.Chain(seed => {
var n = seed.n + 1;
return Tuple.Create(seed.fac, new {n, fac = seed.fac*n});
});
}
Оставить комментарий
6yrop
Читаю тут MIT-овский учебник.В главе Modularity, Objects, and State в первом же подразделе рассказывается, что через введения состояния можно достичь модульности. И приводится пример с вычислением случайных чисел. Вот абзац, где говорится, как хорошо с состоянием (типа модульность) и как плохо без него:
Но ведь этот код легко переписывается и без состояния и с такой же модульностью.