Не могу понять формат массива комплексных значений
Откуда считается спектр, с первого значения?очевидно, первое значение - есть сумма всех чисел на сетке, разделенная (или не разделенная) на число узлов
очевидно, первое значение - есть сумма всех чисел на сетке, разделенная (или не разделенная) на число узлов
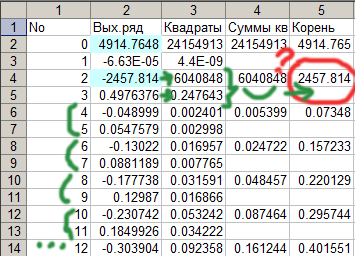
Хорошо, но непонятно, откуда берётся второе число (обведено красным). Напомню, что в пятом столбце я показываю как получаю значения модуля спектра.
Видно, что выделенное число выделяется из общего ряда (см .ниже). Модули спектра получаются из пар вещественное - мнимое значение (пары чисел из второго столбца: 4-5; 6-7; 8-9; 10-11 и т.д.). Пары же 0-1 и 2-3 получаются какими-то неправильными. Ладно, первое число - это как бы нулевой порядок спектра. Его можно не учитывать, а что делать с парой 2-3?

тыб штоль для приличия график функции запостил бы сюда
а то угадывать, почему у тебя в спектре большие значения появляются не имея информации о функции - крайне сложно
зы. вторая гармоника большая, вот и число большое
ззы. если ты сомневаешся в правильности работы бпф (с условием, что он реализован правильно то не стоит.
а то угадывать, почему у тебя в спектре большие значения появляются не имея информации о функции - крайне сложно
зы. вторая гармоника большая, вот и число большое
ззы. если ты сомневаешся в правильности работы бпф (с условием, что он реализован правильно то не стоит.
тыб штоль для приличия график функции запостил бы сюдаOk
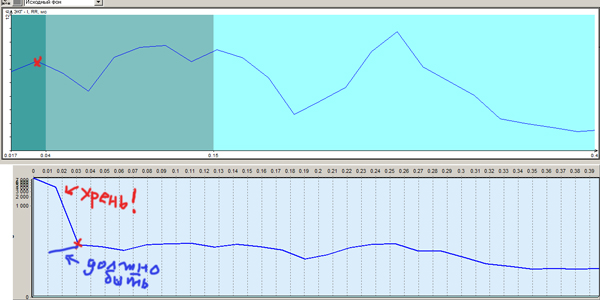
Вверху результаты одной проверенной софтины, внизу - результаты моей програмы на тех же данных. Масштаб лограрифмический в обоих случаях, поэтому не очень хорошо видно, но конфигурация графиков идентична за исключением грёбаного начала. Начало "нормального графика", после которого всё норамально помечено красным крестиком. Синим цветом я от руки нарисовал как примерно должен идти график (внизу).
зы. вторая гармоника большая, вот и число большоеНе может быть, поскольку подавал чистый тестовый сигнал, такая же хрень, да и вообще, для любого сигнала эти первые два числа большими получаются.
ззы. если ты сомневаешся в правильности работы бпф (с условием, что он реализован правильно то не стоит.Работает нормально. Надо только понять, что делать с первыми точками. Первая, как я понимаю, что-то вроде нулевого порядка. Или нет?

А вот дальше не понятно...
я имел ввиду ф-ю, по которой фурье считается
это "гребаное" начало "проверенная" софтина может спокойно урезать и похоже так делает
это "гребаное" начало "проверенная" софтина может спокойно урезать и похоже так делает
Вот, подогнал примерно масштаб своего графика:
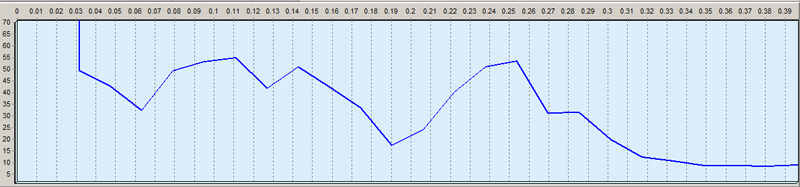

я имел ввиду ф-ю, по которой фурье считаетсяДа ничего она не обрезает. В моей программе не хватает только одной нормальной точки слева и всё ok.
это "гребаное" начало "проверенная" софтина может спокойно урезать и похоже так делает
А функция сложная: берётся электрокардиограмма, выделяются наиболее выраженные зубцы (R-зубцы). По ним строится так называемая интервалограмма. Точки её получаются как набор последовательных интервалов между найденными R-зубцам. Таким образом, по абцисс идёт кол-во интервалов, по ординат - величина интервала, обычно в секундах.
Далее ряд интерполируется так, чтобы кол-во точек интервалограммы соответствовало частоте дискретизации Fs. У меня Fs=250Гц, т.е. за 1 сек берётся 250 отсчётов. За ту же секунду обычно получается 2-3 точки интервалограммы. Недостающие между ними точки дополняются так, как бы интервалограмма была получена с Fs=250Гц. Это нужно для задания необходимого разрешения FFT. Спектр считается эпохами(ансамблями заданными кол-вом интервалов (64,128 и т.д. которые перекрываются через 50%. Перед подачей на вход спектрального анализа к каждому ансамблю отсчётов применяется сглаживающая оконная функция. Я беру ф-цию Ханна. На один ансамбль из 64 R-R интервалов у меня получается 16536 отсчётов. Это соответствует спектральному разрешению 250/16384=0,0153Гц. После расчёта спектров по всем перекрывающимся ансамблям результаты усредняются и выводятся на график.
Всё работает и проверено на сто рядов. Проблема в фиче БПФ-алгоритма. Надо этот момент просечь и всё будет нормально.
блин
ты можешь график этой функции сюда запостить?
ты можешь график этой функции сюда запостить?
Какой функции? Я же показал примеры графиков на реальных данных. Не понимаю. 
А! Интервалограмму показать? Счас пофотошоплю...

Максимум справа соответствует 181 секунде. Масштаб линейный. Колебания очень медленные. Максимум графиков
спектров соответствует 0,4 Гц.

А! Интервалограмму показать? Счас пофотошоплю...

Максимум справа соответствует 181 секунде. Масштаб линейный. Колебания очень медленные. Максимум графиков
спектров соответствует 0,4 Гц.
Да ничего она не обрезаетвполне может, ибо первые гармоники как правило нахуй не нужны и наличие их на графике - значит, что ты остальной спектр не увидишь, даже в логарифмическом масштабе говно выйдет
вполне может, ибо первые гармоники как правило нахуй не нужны и наличие их на графике - значит, что ты остальной спектр не увидишь, даже в логарифмическом масштабе говно выйдетДа говорю же! У меня этот "хвост" получается везде. Сейчас покажу картинку спектра тестового сигнала, который должен быть 0,25Гц.
> У меня этот "хвост" получается везде.
КОНЕШНО! ПОТОМУШТА ТАГ ПРАВЕЛЬНО!
КОНЕШНО! ПОТОМУШТА ТАГ ПРАВЕЛЬНО!
КОНЕШНО! ПОТОМУШТА ТАГ ПРАВЕЛЬНО!Да в хуй не стучит этот хвост.
Вот картинка тестового сигнала, который получен из хитроумного частотно-модулированного сигнала, моделирующего R-зубцы кардиограммы (отдельную программку делать пришлось):
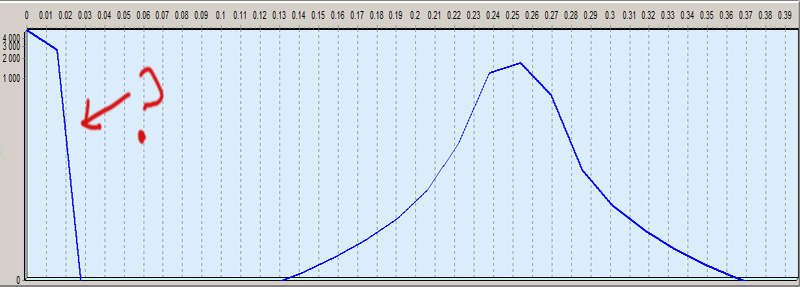
у тебя твои зубцы все положительные, а посему сложи их и получишь нулевую гармонику, то есть, твой всплеск, от которого ты хочешь так избавиться
он никуда не пропадет, он есть, был и будет и так мир устроен!
а твоя мегапрога похоже соображает, что этот всплеск на низких частотах в хуй никому не впился и к спектру применяет какой-нибудь low-pass фильтр, отчего он пропадает и тебе кажется, что его там не должно быть
все, спать
он никуда не пропадет, он есть, был и будет и так мир устроен!
а твоя мегапрога похоже соображает, что этот всплеск на низких частотах в хуй никому не впился и к спектру применяет какой-нибудь low-pass фильтр, отчего он пропадает и тебе кажется, что его там не должно быть
все, спать

в качестве теста: возьми свою кардиограмму, пащетай среднее значение, затем изо всех точек вычти это среднее и вычисли фурье
тебя приятно удивит нулевое значение нулевой гармоники
тебя приятно удивит нулевое значение нулевой гармоники
в качестве теста: возьми свою кардиограмму, пащетай среднее значение, затем изо всех точек вычти это среднее и вычисли фурьеУ меня предусмотрено вычитание постоянной состовляющей, но я это место закомментировал. Сейчас попробую...
тебя приятно удивит нулевое значение нулевой гармоники
Убрал постоянную составляющую.
Вверху "спектр до", внизу - "спектр после".
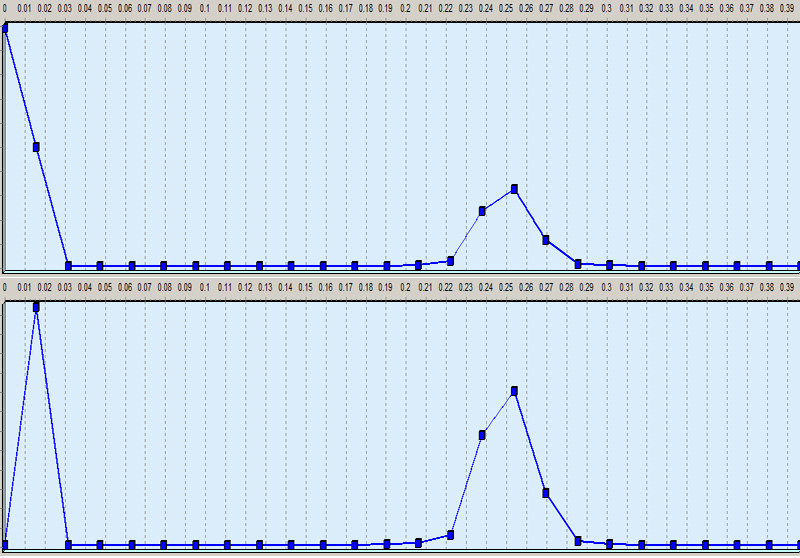
Я почти вкурил. Спасибо большое.
Так оставшийся всплеск откуда? Гармоника?
Вверху "спектр до", внизу - "спектр после".

Я почти вкурил. Спасибо большое.
Так оставшийся всплеск откуда? Гармоника?
> Гармоника?
первая, А*e^(i*pi*w/W где W - максимальная частота (Найквиста w - от 0 до W, A - есть значение всплеска
первая, А*e^(i*pi*w/W где W - максимальная частота (Найквиста w - от 0 до W, A - есть значение всплеска
В последний раз "на пальцах", плз, откуда она берется. Я гуманитарий, сделай скидку. Прости, что отвлекаю от приготовлений ко сну. 
Частота Найквиста я знаю что такое и откуда эффект стробирования берётся. А здесь что?

Частота Найквиста я знаю что такое и откуда эффект стробирования берётся. А здесь что?
на пальцах: любую периодическую функцию можно представить в следующем виде:
(фазы не пишу, в топку их) f(x) = A + B*sin(pi*x) + C*sin(2*pi*x) + D*sin(3*pi*x) + E*sin(4*pi*x) + дохуя
так вот, твой спектр - есть: сначала A(нулевая гармоника потом B(первая потом С(вторая D, E, F, ... и так до бесконечности
че-то спать расхотелось
(фазы не пишу, в топку их) f(x) = A + B*sin(pi*x) + C*sin(2*pi*x) + D*sin(3*pi*x) + E*sin(4*pi*x) + дохуя
так вот, твой спектр - есть: сначала A(нулевая гармоника потом B(первая потом С(вторая D, E, F, ... и так до бесконечности
че-то спать расхотелось

Вот этот мой тестовый сигнал 0,25Гц. Вверху - импульсный сигнал; внизу - периодограмма, полученная из импульсного сигнала.
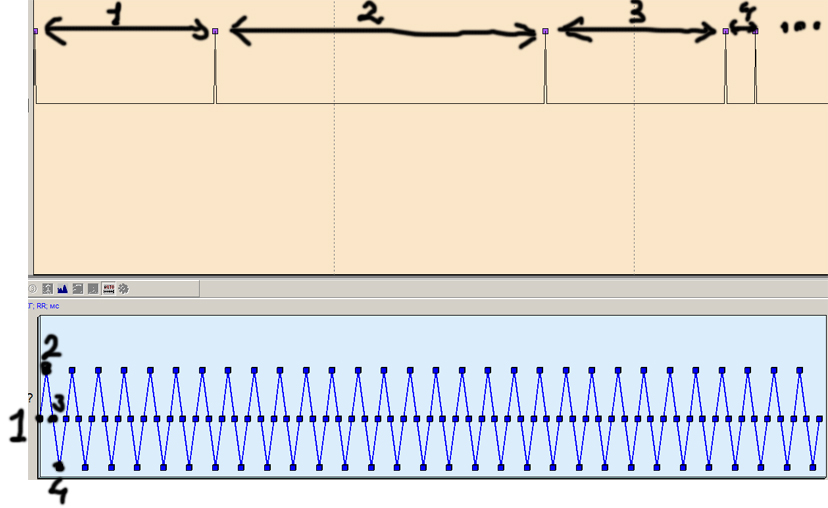

че-то спать расхотелосьА как графически, в этом конкретном случае, эта гармоника проявляется?
Ладно, всё, закругляюсь. Тебе, наверное, завтра работать. Я-то "свободный художник" сейчас.

Погонял FFT на разных тестовых сигналах. Всё правильно. Я протормозил. Мог и сам догнать.
Но как же в моём случае проще всего подавить первую гармонику? Постоянную составляющую я убираю без проблем.
Нулевой порядок пёр из-за "подставки" постоянки в сигнале? Это понятно.
Первая-то гармоника где графически на функции?
Но как же в моём случае проще всего подавить первую гармонику? Постоянную составляющую я убираю без проблем.
Нулевой порядок пёр из-за "подставки" постоянки в сигнале? Это понятно.
Первая-то гармоника где графически на функции?
если бы была только первая гармоника, то график - полпериода синуса
а т.к. у тебя есть и другие гармоники, то ее вполне можно и не увидеть
насчет как убрать - домножай свой спектр на (1-e^x/a)^n)^2 где a и n подбирать, чтобы давились ненужные гармоники, а нужные практически не изменялись бы
а т.к. у тебя есть и другие гармоники, то ее вполне можно и не увидеть
насчет как убрать - домножай свой спектр на (1-e^x/a)^n)^2 где a и n подбирать, чтобы давились ненужные гармоники, а нужные практически не изменялись бы
домножай свой спектр на (1-e^x/a)^n)^2)Блин.

Ты еще сигнал свернуть посоветуй.

У меня этот "хвост" получается везде.Можно еще параметрами кардиографа поинтересоваться. Может, у него выпрямитель гудит на 0,48 Гц.
что такое?
Да нет, ничего.
Просто напугала фильтрация.
Такой простой фильтр, который вырежет вторую гармонику, еще и последующие серьезно затронет.
Просто напугала фильтрация.
Такой простой фильтр, который вырежет вторую гармонику, еще и последующие серьезно затронет.

> серьезно
я там параметры фильтра оставил на выбор по усмотрению
такшто "если очень захотеть, можно в космос полететь"
я там параметры фильтра оставил на выбор по усмотрению
такшто "если очень захотеть, можно в космос полететь"

Все равно у экспоненты не будет точки перегиба. 

Тут, по-моему, нужен не highpass, а lo-shelf, как минимум. Или вообще двухполосный эквалайзер.


Тут, по-моему, нужен не highpass, а lo-shelf, как минимум. Или вообще двухполосный эквалайзер.
Оставить комментарий
dimon72
У меня есть исходник алгоритма БПФ вещественной функции. Вот описание алгоритма:(ссылка: http://alglib.sources.ru/fft/realfft.php%29.
---------------------------------------------------------------------------------------------------------------------------
Этот алгоритм является адаптацией алгоритма БПФ на случай вещественной функции. В принципе, можно провести БПФ вещественной фунции, расматривая её, как комплексную с нулевой мнимой частью, но такой подход неэффективен. Есть более эффективный подход, который позволяет в два раза повысить скорость за счет сведения задачи к задаче с в два раза меньшим числом значений, но с ненулевой мнимой частью.
На входе процедура получает параметры:
* tnn - число значений функции. Должно быть степенью двойки.
* a - массив из tnn вещественных чисел, нумерация элементов от 0 до tnn-1. Если мы проводим прямое преобразование, этот массив задает tnn значений функции (не забываем, что функция вещественная, а не комплексная). Если преобразование обратное, то здесь хранятся соответствующие частоты (более подробно формат хранения приведен ниже, на картинке).
* InverseFFT - направление преобразования. Если мы проводим прямое преобразование, то устанавливаем параметр в False. Устнавливаем его в True, если преобразование обратное.
На выходе:
* a - содержит результат преобразования. Если проведено прямое преобразование, то здесь находятся частоты (более подробно формат хранения приведен ниже, на картинке при обратном преобразовании здесь хранятся значения функции.
Рассмотрим более подробно формат массива. Пусть у нас есть N значений функции, расположенных с интервалом Delta. Каждому значению hk соответствует определенный момент времени tk .
После проведения преобразования Фурье мы получаем массив комплексных значений (пар вещественных чисел в котором хранятся наши коэффиценты Hn (вспомним формулы в начале статьи). Существует зависимость между номером i и соответствующей ему частотой fi , между коэффициентом Hi и значением преобразования Фурье (непрерывного преобразования) на соответствующей частоте fi :
Если сравнить эту картинку с аналогичной для БПФ комплексной функции, то мы заметим, что частоты с f-1 по f-N/2+1 куда-то исчезли, а от частот f0 и fN/2 остались только вещественные части, занявшие прежнее место комплексной частоты f0 . Причиной этого являются свойства симметрии преобразования Фурье: для вещественной функции h(t) верно, что H(-f) = H ·(f).
Таким образом, частоты с f-1 по f-N/2+1 уже не несут в себе новой информации, т.к. получаются комплексным сопряжением своих симметричных близнецов, а у частот f0 и fN/2 мнимые части равны нолю.
---------------------------------------------------------------------------------------------------------------------------
Вопрос состоит в следующем.
В итоге, на выходе я получаю спектральные компоненты в виде модуля, который считается как корень из суммы квадратов реальной и мнимой частей выходного ряда приведённого алгоритма. Что мне делать с первыми двумя числами? Что они обозначают?
Допустим, я подаю на вход 1024 отсчёта. Таким образом, имею 1024/2=512 значений сетки преобразования. Например, при частоте дискретизации Fs=250 шаг сетки преобразования получается 250/1024=0,24Гц.
Я не совсем понял что мне делать с первыми значениями выходного алгоритма.
Вот пример фрагмента выходного ряда (столбец 2) и того, как я получаю выходные значения.
Описание: столбец 3 - это квадраты чисел из столбца 2; столбец 4 - суммы двух чисел из левого столбца (столбца 3); столбец 4 - корень из чисел столбца 3.
Отмеченные маркером числа как-то не вписываются в результаты. Что делать?
Еще вопрос. Откуда считается спектр, с первого значения? То есть, для приведённого примера:
0,24; 0,48; 0,72; 0,96 и т.д. до 125Гц или:
0; 0,24; 0,48; 0,72; 0,96 и т.д. до 125Гц ?